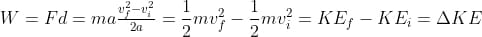- What is Work-Energy Theorem?
- Derivation of Work-Energy Theorem
- Derivation of Work-Energy Theorem: Step-by-Step
- Illustrated Examples on Work-Energy Theorem
- FAQs on Work-Energy Theorem
What is Work-Energy Theorem?
The work-energy theorem defines the relation between kinetic energy and total work. The sum of all the work is equivalent to the changes that occur in the kinetic energy. It can be extended to describe the rotational kinetic energy of stiff bodies and the work of the kinetic energy. The kinetic energy of an object can be defined as the energy it possesses due to the external force of the object.
In simple words, it is the work that is required to accelerate the object or to move the object from rest to motion. Examples of kinetic energy include a walking person, an apple falling from the table, books falling from the shelf, thrown football, etc. It can be perceived from the movement of an object or a particle.
Derivation of Work-Energy Theorem
Work done is said to be done when an external force acts on an object. If the displacement is 0, it is assumed that no work has been done. Work is defined as the change in kinetic energy, and it includes both displacement and force.
The work-energy theorem can be expressed as:
Here, ΔK represents the change in kinetic energy,
W is the work done; the unit of work is the joule.
Derivation of Work-Energy Theorem: Step-by-Step
The equation of motion is written as:
Equation of Motion
| V2 = u2 + 2 as |
|
|---|---|
| v |
Final velocity |
| u |
Initial velocity |
| a |
Acceleration (assumed as constant) |
| s |
Displacement |
The above equation can be rewritten as
- V2 – u2 = 2 as
After multiplying both the sides by m/2, we get the following equation –
- ½ mv2 – ½ mu2 = m a.d = F.d
We already know that W = F.d and Kinetic Energy = (mv2)/2
The equation will be derived as:
- Kf – Ki = W
By this equation we get,
- ΔK = W
- ΔK = Kf – Ki (this equation shows the change in kinetic energy.
After calculating the work-energy theorem, we can say that the work is equivalent to the change in an object’s kinetic energy.
Derivation of the work-energy theorem in class 11
The chapter of 'work, energy, and power' holds a significant weightage of 6 marks. It consists of one objective type question of 1 mark, one very short question of 2 marks, and one short question of 3 marks bringing a total of up to 6 marks.
Illustrated Examples on Work-Energy Theorem
Example 1) Illustrate the work related to displacement and force acting on an object.
Answer – The illustration is as follows:
Example 2) State the formula of the work-energy theorem.
Answer – The formula of the work-energy theorem is W = ΔK.
Example 3) State the formula used for the work done by a variable force.
Answer – The formula is ∆W =F (x) ∆x.
[Image Courtesy: NCERT]
FAQs on Work-Energy Theorem
Q: A body of mass 2 kg initially at rest moves under the action of an applied horizontal force of 7 N on a table with coefficient of kinetic friction = 0.1. Compute the (a) work done by the applied force in 10 s, (b) work done by friction in 10 s, (c) work done by the net force on the body in 10 s, (d) change in kinetic energy of the body in 10 s, and interpret your results.
A: Given, mass of the body, m = 2 kg
- Horizontal force applied, F = 7 N
- Coefficient of friction, μ = 0.1
- Acceleration, a = F/m = 7/2 = 3.5 m/s2
- Frictional force, f = μR = μmg = 0.1 X 2X 9.807 = 1.96 N
- Retardation produced by the frictional force, ar = -f/m = -1.96 /2 = 0.98 m/s2
- The net acceleration by which the body moves forward an = a - ar = 3.5 – 0.98 = 2.52 m/s2
- Distance moved by the body in 10 s is given by s = ut + (1/2)an t2 = 0 X 10 +(1/2) X 2.52 X 102 = 126 m
- (a) Work done in 10 s is given by
- W = Force X displacement = 7 X 126 = 882 J
- (b) Work done by friction in 10 s is given by
- W = -f X s = -1.96 X 126 = - 247J
- (c) Work done by the net force,
- W = (F-f) = (7 – 1.96 ) X 126 = 635 J
- Kinetic energy is given by the equation
- KE = (1/2)mv2 where v is the final velocity
- From the equation v = u + at we get after 10 s, v = 0 + 2.52 X 10 = 25.2 m/s
- Final kinetic energy = (1/2) X 2 X 25.22 = 635 J
- Initial kinetic energy = (1/2) x 2X 02 = 0
- Change in kinetic energy = 635 – 0 = 635 J
- Hence the work done by the net force = change in kinetic energy
Q: Given in Fig. 6.11 are examples of some potential energy functions in one dimension. The total energy of the particle is indicated by a cross on the ordinate axis. In each case, specify the regions, if any, in which the particle cannot be found for the given energy. Also, indicate the minimum total energy the particle must have in each case. Think of simple physical contexts for which these potential energy shapes are relevant.
A:
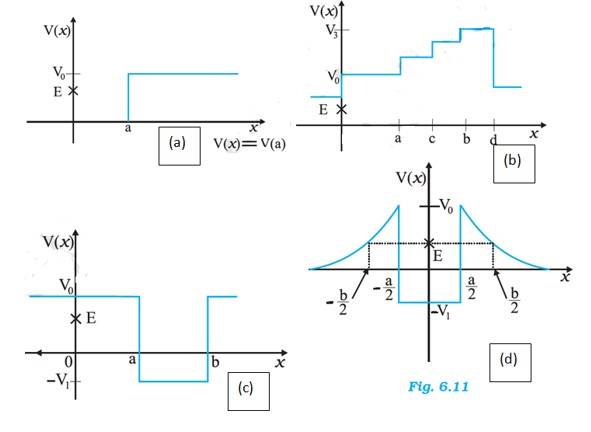
We know the total energy E is given by E = Kinetic energy (KE) + Potential energy (PE)
- In figure (a), we have at x=0, the potential energy is zero. So KE is positive. At x>a, the potential energy has a value greater than E, so the KE becomes 0. Thus the particle will not exist in the region x>a. Minimum total energy is zero.
- (b) For the entire x-axis, PE >E, the KE of the object would be negative. Thus the particle will not exist in this region.
- (c) In x=0 to x=a and x>b, PE is greater than E, so he KE has to be negative. The object cannot exist in this region.
- (d) For x=-b/2 to x =-a/2 and x=a/2 to x=b/2, KE is positive and the PE
Q: Answer the following : (a) The casing of a rocket in flight burns up due to friction. At whose expense is the heat energy required for burning obtained? The rocket or the atmosphere? (b) Comets move around the sun in highly elliptical orbits. The gravitational force on the comet due to the sun is not normal to the comet’s velocity in general. Yet the work done by the gravitational force over every complete orbit of the comet is zero. Why ? (c) An artificial satellite orbiting the earth in very thin atmosphere loses its energy gradually due to dissipation against atmospheric resistance, however small. Why then does its speed increase progressively as it comes closer and closer to the earth ? (d) In Fig. 6.13(i) the man walks 2 m carrying a mass of 15 kg on his hands. In Fig. 6.13(ii), he walks the same distance pulling the rope behind him. The rope goes over a pulley, and a mass of 15 kg hangs at its other end. In which case is the work done greater ?
A:
- (a) As per the law of conservation of energy,
- Total energy = potential energy + kinetic energy = mgh + 1/2mv2
- When the casing burns, mass reduces, resulting in drop of energy. Hence the energy for burning of casing is drawn from the rocket.
- (b) The force due to gravity is a conservative force. The work done on a closed path for a conservative force is zero. Hence, for every complete orbit of the comet, the work done by the gravitational force is zero.
- (c) The potential energy of the satellite revolving the Earth decreases as it approaches the Earth and since the system’s total energy should remain constant, the kinetic energy increases. Hence the satellite velocity increases when it approaches the Earth.
- (d)
-
- Give, m = 15 kg, displacement, s = 4m
- From the relation, work done, W = F x s X cosθ where θ is the angle between the force and displacement. Here F = mg, hence, W = mgscosθ = 15 X 9.8 X 4 X cos 90° = 0
- Mass = 15 kg, s = 4 m, the applied force direction is same as the direction of the displacement, θ = 0 . Hence W = 15 X 9.8 X 4 X cos 0° = 588 J
Q: Underline the correct alternative: (a) When a conservative force does positive work on a body, the potential energy of the body increases/decreases/remains unaltered. (b) Work done by a body against friction always results in a loss of its kinetic/potential energy. (c) The rate of change of total momentum of a many-particle system is proportional to the external force/sum of the internal forces on the system. (d) In an inelastic collision of two bodies, the quantities which do not change after the collision are the total kinetic energy/total linear momentum/total energy of the system of two bodies.
A:
- (a) When a conservative force does positive work on a body, the body gets displaced in the direction of the force, it moves towards the centre of the force, thus resulting in decrease of potential energy.
- (b) When the work done by a body against friction, it reduces its velocity. Hence kinetic energy decreases.
- (c) The momentum cannot be changed by the internal forces on the system; the change of momentum is proportional to the external force.
- (d) The total linear momentum does not change in an elastic collision.
Q: What do you mean by Kinetic energy?
A: Kinetic energy of an object can be defined as the energy it possesses due to the object’s external force. In simple words, it is the work that needs to be done to accelerate the object or to move the object from rest to motion.
Q: What is the S.I. unit of Kinetic Energy?
A: The unit of kinetic energy is Joule.
Q: What is the principle of the work-energy theorem?
A: The principle of work-energy states that the positive work done on an object causes an increase in a stiff body’s kinetic energy.
Q: What is the formula used to calculate work?
A: The formula used to calculate work is W = F x D.
Q: What is the formula of Kinetic energy?
A: The formula of kinetic energy is K = ½ mv2.
Physics Work, Energy and Power Exam
Student Forum
Popular Courses After 12th
Exams accepted
CA FoundationExams accepted
ICSI ExamExams accepted
BHU UET | GLAET | GD Goenka TestBachelor of Business Administration & Bachelor of Law
Exams accepted
CLAT | LSAT India | AIBEExams accepted
IPMAT | NMIMS - NPAT | SET
Exams accepted
BHU UET | KUK Entrance Exam | JMI Entrance ExamBachelor of Design in Animation (BDes)
Exams accepted
UCEED | NIFT Entrance Exam | NID Entrance ExamBA LLB (Bachelor of Arts + Bachelor of Laws)
Exams accepted
CLAT | AILET | LSAT IndiaBachelor of Journalism & Mass Communication (BJMC)
Exams accepted
LUACMAT | SRMHCAT | GD Goenka Test