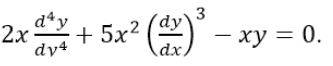Differential Equations Applications: Overview, Questions, Preparation

Differential Equations

d(y)d(x) = f(x) = y' 

Or on the other hand 

y'=d(y)d(t) 

Or then again 

f(x,y) = d(y)d(x) = d(y)d(t) = y' 

Or then again 

x1\(\frac{d(y)}{d(x1)}\) + x2 \(\frac{d(y)}{d(x2)}\) = y 

Where x is the free factor 

What's more, y is the reliant variable, as its capacity is subject to the estimations of x. 

Y' means one subsidiary. Also, y'', y''', …, so on, indicating the number of subsidiaries for all estimations of x. 

There are numerous utilisations of differential conditions in math in light of these recipes.

Types of Differential Equations:

Essentially, there are two sorts of differential conditions; 

Conventional Differential Equation(ODE) 

The conventional differential condition includes a connection between one genuine variable, which is autonomous state x, and one ward variable state y and amount of subordinates y', y'', y'''… regarding the estimation of x. 

f(x) = y = d(y)d(x) 

The most elevated subordinate which happens in the condition is the request for the conventional differential condition. The equation can compose tribute for the nth request as; 

F(x,y,y',… .,yn) = 0 

For instance, as indicated by the Newton law of cooling, the temperature adjustment is straightforwardly relative to the distinction between the temperature of the hot item or body and the air temperature. Consequently, as far as the differential condition, we can call it as; 

dT/dt ∝ (T – Ta) 

Or on the other hand 

dT/dt = k (T – Ta) 

Where k is relatively consistent and T is the temperature of the article, and Ta is the air temperature. 

Fractional Differential Equation(PDE) 

In the fractional differential condition, there is more than one autonomous variable in contrast to the common differential condition. 

For instance: 

dz/dx + dz/dy = 2z is a halfway differential condition of one request. 

d²u/dx² + d²u/dy² + 2x + 2y – z is a halfway differential condition of the second request.

Applications:

We can depict the differential conditions applications, in actuality, regarding: 

Remarkable Growth 

For remarkable development, we utilise the recipe; 

G(t)= G0 ekt 

Let G0 is positive, and k is steady at that point. 

dGdt= k 

G(t) increments with time 

G0 is the worth when t=0. 

G is a remarkable development model. 

Remarkable decrease or rot 

R(t) = R0 e-kt 

At the point when R0 is positive, and k is consistent, R(t) is diminishing with time, 

dRdt = - k 

R is the remarkable decrease model. 

In class 12: In chapter differential equations, various equations and derivations have been explained precisely along with the questions.
The chapter has a weightage of 35 Marks.

1. Solve (cox x cos y – cotx) dx – sin x sin y dy = 0

Solution.

sin x cos y = ln (c sin x)

2. Solve the differential equation dy – x dx = 0, if the curve passes through (1, 0)?
Solution.                      

x² – 2y – 1 = 0

3. Solve (y – √(x² + y²)) dx – x dy = 0
Solution.

√(x² + y² ) + y = C

• Ordinary Differential Equations.
• Partial Differential Equations.
• Linear Differential Equations.
• Nonlinear differential equations.
• Homogeneous Differential Equations.
• Nonhomogeneous Differential Equations

Q: Determine the order and degree of the following:

Q: Define differential equation with example

Q: What kind of differential equations are?

Q: While settling an Ordinary Differential Equation utilising the one-sided Laplace Transform, it is conceivable to tackle if there is no capacity in the correct hand side of the condition in standard structure and if the underlying conditions are zero.

Q: Which equation is the exact direct equation?