Application of Integrals: Overview, Questions, Preparation

Integration is the reverse function of a differential and is represented by  ∫. It has numerous applications in the fields of mathematics and science and some of these applications are:-

Area under a curve

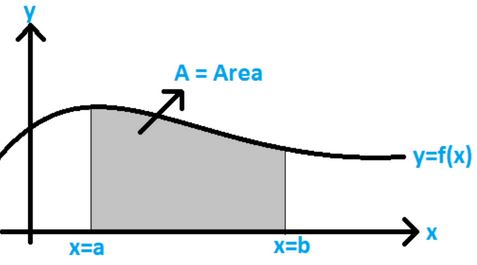
To understand how we can find the area under a simple curve, consider a curve function:

y = f(x) 

On a graph, draw the curve and two straight lines x=a and x=b ( where b>a ). Imagine the area bounded by the curve between the two straight lines as a collection of several thin strips.
Consider a strip and assign its height as y and its breadth as dx. This arbitrary strip is called the Elementary Area.

Area of the strip: dA = y dx

y = f(x) and dx is a small value between a and b

Now, the area under the curve is the total area of all the individual strips.

Total area:, A =_a∫^b dA = _a∫^b y dx =  _a∫^b f(x) dx 

The area between a curve and a line 

The same formula can be applied to find the area bounded by a circle, parabola, or an ellipse and a line. Represent the lines and the curves on the x-y axis before solving the problem.

The area between two curves

Consider two curves represented by y = f(x)  and y = g(x)
These curves will intersect at point x=a and x=b

Area between curves = ∫ab  [f(x) -g(x)] dx
Where f(x) > g(x) in [a,b]

Details about the topic

Integration and its applications are introduced to higher class levels and is taught to students in grade 12 as a part of Calculus. The concepts of integrals are used in different scientific modules and complex mathematical functions.

Find the area of the region bounded by the curve y² = x and the lines x = 1, x = 4, and the x-axis in the first quadrant.

y² = x   
y = √x
Area under the curve = ₁∫⁴ y dx  = ₁∫⁴ √x dx

=   [x^3/2   ÷ 3/2 ]₁⁴  
=  ⅔  [4^3/2 - 1^3/2 ] = 14/3 unit²

2. The area between x = y² and x = 4 is divided into two equal parts by the line x = a. Find the value of a.

Solution.

y² = x   

y = √x

Area 1 = area between origin and line x=a

Area 2 = area between line x=a and x=4 

Area 1 = Area 2

₀∫^a √x dx = _a∫⁴ √x dx 

⅔ a^3/2 = ⅔  [ 8 - a^3/2 ]

a^3/2 =4

a = 4^2/3    

3. Using integration find the area of the triangular region whose sides have the
equations y = 2x + 1, y = 3x + 1 and x = 4.

Solution. Use the equations to find the vertices of the triangle

A (0,1)

B (4,13)

C (4,9)

The area of the triangle is obtained by subtracting the area under the line y = 2x + 1 from the area under the line y = 3x + 1

= ₀∫¹ (3x + 1)dx - ₀∫¹ (2x + 1)dx

= [3x²/2 + x - (2x²/2 +x)  ]₁⁴  
= 8 unit²

Q: What can integration be used for?

Q: How can you calculate the area bounded by a curve on the y axis?

Q: What function represents a circle?

Q: What is the area enclosed by the ellipse x/a2 + y/b2 =1 ?

Q: What is the area enclosed by the circle x2 +y2= a2?