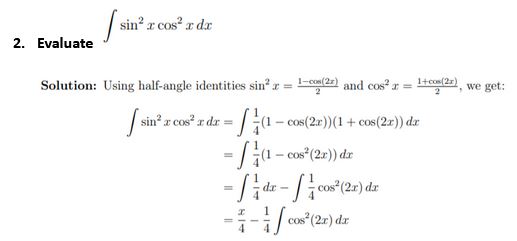Riemann Integral: Overview, Questions, Preparation

Let us assume that f is a function characterised over a shut stretch addressed by [a, b]. Assume f is a non-negative and persistent function. The integral of f regarding x implies the zone between the diagram of f and X-pivot. This territory would be called the definite integral of a function f from a to b.

The Riemannian technique for deciding this region (or definite integral) is: "on the off chance that the zone is partitioned into square shapes of minuscule expansiveness, at that point it is easier to ascertain the region of such square shapes, and afterwards we can add them up." See the accompanying graph.

It is undeniable that if these square shapes are exceptionally tight, at that point, the estimation blunder would be insignificantly little. For the smaller square shapes, the deliberate approximated zone may join to a number known as the zone under the bend of the function f. On the off chance that we do not draw minuscule square shapes, at that point, this strategy will, in general, separate. To make the Riemann system exact, we may decide the widths of square shapes by parting the given span [a, b] into more modest parts.

Sums

Let us comprehend a couple of different ideas before finding out about the Riemann aggregate. 

Parcel: 

Assume a shut stretch [a, b] ∈ R. 

The parcel of this stretch is supposed to be an arrangement of the accompanying structure: 

a = x0

Where, each [xi,xi+1 ] is known as a sub-stretch. 

Norm: 

The most significant sub-stretch length is a standard or a cross-section; for example, standard = max. 

Labelled Partition: 

For stretch [a, b], a parcel P(x, t) alongside an arrangement of limited numbers t0,t1,…,tn-1, is known as a labelled segment if it fulfils the condition that, ti ∈ [xi, xi+1] for each I. 

Riemann Sum: 

The Riemann amount of a genuine esteemed function f on the span [a, b] is characterised as the amount of 'f' concerning the labelled parcel of [a, b]. For example,

Formula:

Let f be a genuine esteemed function over the span [a, b] and let L be a genuine number. At that point, f is called integrable inside [a, b] if and just if there is a δ > 0 for each ϵ > 0 with the end goal that for each segment having a property that ||P||

|S(f,P)−L|

Importance and Weightage

In chapter Integral, the Riemann integral has been explained briefly along with its properties and details. Questions have also been given for it. It has a weightage of 35 marks in the exam.

2. Evaluate

Q: Define Riemann integral function.

Q: What are the types of integrals?

Q: Are all continuous functions Riemann integrable?

Q: Is Thomae function differentiable?

Q: What does it mean for a function f to be an Anti-derivative of a function f on an interval?