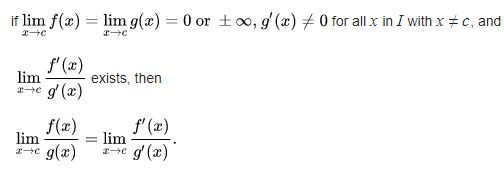L Hospital Rule: Overview, Questions, Preparation

This chapter has multiple topics listed below:

Limits and Derivatives Derivatives Limits L Hospital Rule Quotient Rule Indeterminate Forms Limits and Continuity

Updated on Aug 13, 2021 14:10 IST

Table of Contents

What is L’Hospital’s Rule?
Weightage of L’Hospital’s Rule
FAQs on L’Hospital’s Rule

What is L’Hospital’s Rule?

The most relevant rule of Mathematics is L’Hospital’s Rule. The derivatives are used to determine the limits that cover the indeterminate types in this rule. In this post, along with illustrations, we will address the formula and facts for the L’Hospital law.

L’Hospital’s rule is an overall technique for assessing uncertain structures, for example, 0/0 or ∞/∞. To assess the restrictions of vague structures for the subordinates in analytics, L’Hospital’s standard is utilised. L’Hospital’s rule can be applied more than once. You can apply this standard still, and it holds any uncertain structure each time after its applications. On the off chance that the issue is out of the vague structures, you can’t have the option to apply L’Hospital’s rule.

Rule Evidence

By utilising the Extended Mean Value Theorem or Cauchy’s Mean Value Theorem, L’Hospital’s rule can be demonstrated.

If f and g are two persistent capacities on the span [a, b] and differentiable on the stretch (a, b), then

f'(c)/g'(c) = [f(b)- f(a)]/[g(b)- g(a)]

with the end goal that c have a place with a (a, b).

Expect that the two capacities f and g are characterised on the span (c, b) so that f(x)→0 and g(x)→0, as x→c+.

Be that as it may, we have f'(c)/g'(c) keeps an eye on limited cutoff points. The capacities f and g are differentiable, and f'(x) and g'(x) exists on the set [ c, c+k], and furthermore f' and g' are consistent on the span [c, c+k] furnished with the conditions f(c)= g(c) = 0 and g'(c) ≠ 0 on the stretch [c, c+k].

Rule Uses

Utilising the L Hospital rule, we can tackle the issue in 0/0, ∞/∞, ∞ – ∞, 0 x ∞, 1∞, ∞0, or 00 structures. These structures are known as vague structures. To eliminate the vague structures in the issue, we can utilise the L Hospital rule.

Weightage of L’Hospital’s Rule

L Hospital Rule is an integral part of the maths syllabus of Class 11 and is relevant not just for Class 11^th exams but also for various engineering exams such as JEE. Here, focused on the class 11^th maths syllabus, a summary of L Hospital rules and uses is given, which will help quickly learn the relevant terms and achieve good marks in exams.

FAQs on L’Hospital’s Rule

Q: How would you utilise the L Hospital rule?

A: L’Hospital’s rule discloses to us that if we have an uncertain structure 0/0 or ∞/∞ we should separate the numerator and separate the denominator and afterwards take the breaking point.

Q: Will L’Hospital’s standard be applied as far as possible?

A: Review that L’Hôpital’s Rule is utilised with vague restrictions that have the structure 00 or ∞∞. It doesn’t tackle all cutoff points. Even rehashed utilisation of the standard doesn’t help us discover the breaking point esteem in some cases.

Q: For what reason is the L Hospital Rule significant?

A: L’Hospital’s standard is the conclusive method to disentangle the assessment of cutoff points. It doesn’t straightforwardly assess limits, yet possibly disentangles assessment whenever utilised suitably.

Q: When can the L’Hospital’s standard not be utilised?

A: L’Hopital’s standard possibly applies when the articulation is vague, for example 0/0 or (+/ - limitlessness)/(+/ - endlessness). So quit applying the standard when you have a definable structure.

Q: Would 0 be able to be a breaking point?

A: To state the breaking point exists, the capacity needs to move toward a similar worth paying little heed to which course x comes from. Since that isn’t valid for this capacity as x methodologies 0, the breaking point doesn’t exist.