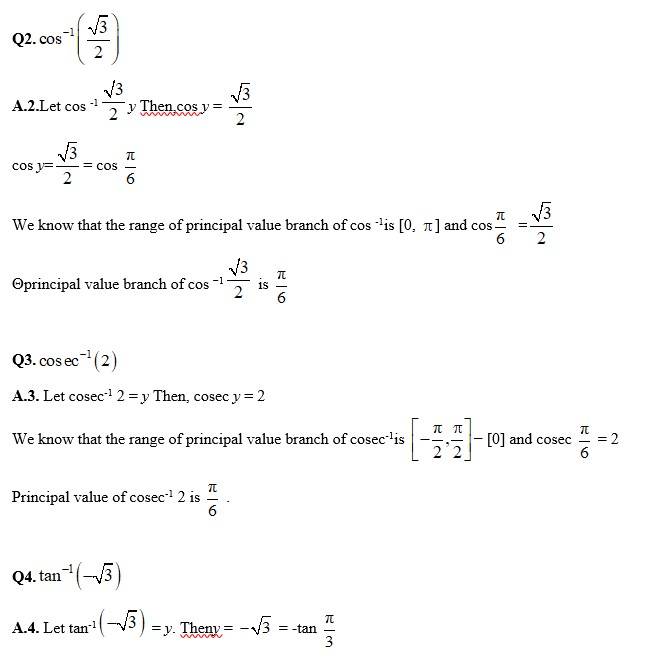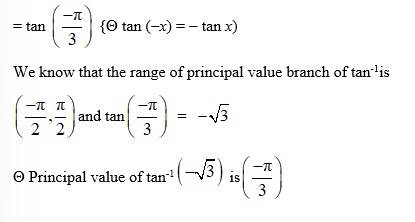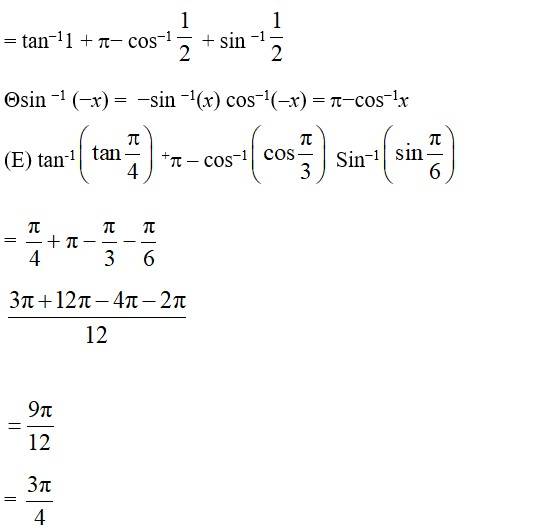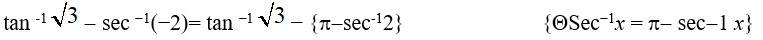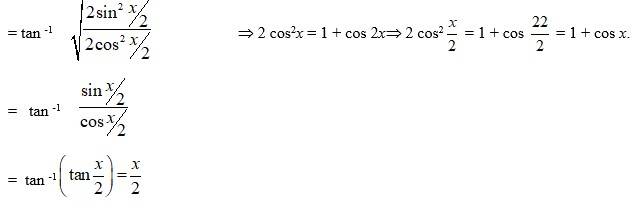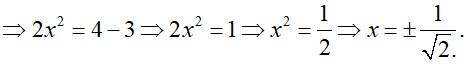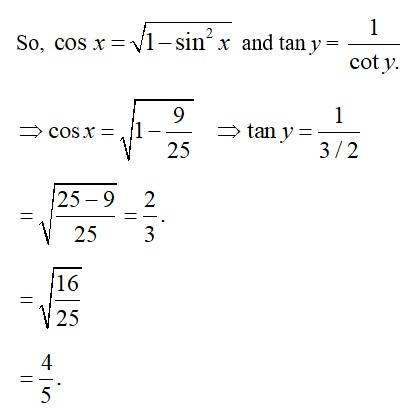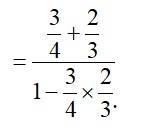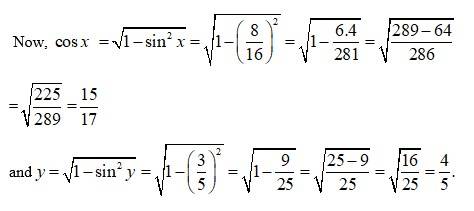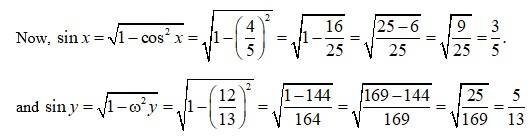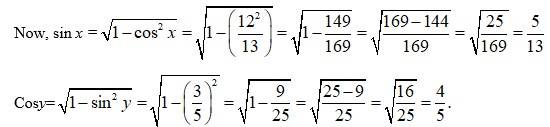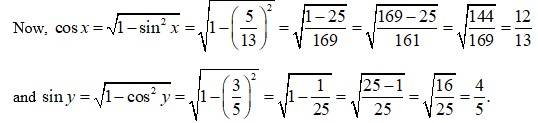Class 12 Chapter 2 Inverse Trigonometric Function NCERT Solutions: Shiksha brings complete class 12 Math NCERT solutions for Chapter 2 Inverse Trigonometric Function to help students. Class 12 Math Chapter 2 Inverse Trigonometric Function is a vital chapter, its concepts are used in calculus, matrices and determinants, physics numerical, and many other important places.
Shiksha provides detailed Inverse Trigonometric Function NCERT Solutions prepared by our experts. Class 12 Math Chapter 2 Inverse trigonometric function is very important for both board and entrance exam students since ITF concepts are used in various other chapters. Students can access the complete Exercise-wise NCERT Class 12 chapter 2 solution PDF on this page.
Students can use the Inverse Trigonometric Function Class 12 Math Solution PDF to strengthen their concepts for CBSE Boards as well as other Entrance exams such as JEE Main, MHT CET, etc. Students should also check the Class 11 Chapter 3 trigonometric function NCERT solutions to get a better understanding of inverse trigonometric functions.
Inverse trigonometric functions are defined as the inverse of basic trigonometric functions; sine, cosine, tangent, cotangent, secant, and cosecant functions. Students can access the complete Class 11 Math chapter-wise Solutions and Class 12 Chapter-wise Math solutions on Shiksha. For more information check below;
| Related Important Math Chapter Solutions | ||
|---|---|---|
| Class 11 Chapter 3 Trigonometric Functions | Class 11 Chapter 2 Relation and Function Solutions | Class 12 Chapter 8 Application of Integrals |
- Class 12 Math Chapter 2 Inverse Trigonometric Function: Key Topics, Weightage & Important Formulae
- Class 12 Math Chapter 2 Inverse Trigonometric Function Solution PDF: Free Download
- Class 12 Math Chapter 2 Inverse Trigonometric Function Exercise-wise Solutions
- Class 12 Math Chapter 2 Inverse Trigonometric Function Exercise 2.1 Solutions
- Class 12 Math Chapter 2 Inverse Trigonometric Function Exercise 2.2 Solutions
- Class 12 Math Chapter 2 Inverse Trigonometric Functions Miscellaneous Exercise Solutions
- Class 12 Math important reference books and preparation Tips
Class 12 Math Chapter 2 Inverse Trigonometric Function: Key Topics, Weightage & Important Formulae
Chapter 2 Inverse Trigonometric function carries 5-6 marks in CBSE Board Exams, often short-answer or value-based questions are asked from this chapter. Inverse Trigonometric Functions have a moderate weightage in competitive exams; however, its concepts are frequently used in integral calculus problems.
This chapter includes inverses of trigonometric functions like sine, cosine, and tangent. Check the key topics of this chapter below;
- Inverse trigonometric functions: sin⁻¹(x), cos⁻¹(x), tan⁻¹(x), cosec⁻¹(x), sec⁻¹(x), cot⁻¹(x)
- Properties: Principle value, real value, domain, range, and co-domain of inverse trigonometric functions
Check out Dropped Topics of Inverse Trigonometric Function: 2.3 Properties of Inverse Trigonometric Functions (Except sin (sin-1 x) = x, x ∈ [-1, 1] sin-1 (sin x) = x, x ∈ [-π/2, π/2], Page 45 – 47 Examples 4, 7 and 8; Alternative Solution of Example 5, Page 47-48 Ques. 3, 4, 6, 12, 14, 15, Page 49-51 Examples 10, 11, 12, 13, Page 51-52 Ques. 8, 12, 17 (Miscellaneous Exercise), Page 53 Summary Points 8–13
Read more: Most scoring topics in Mathematics for JEE Main
Inverse Trigonometric Function Important Formulae for CBSE and Competitive Exams
Basic Properties
Domain and Range of ITF
| Function | Domain | Range |
|---|---|---|
|
|
|
|
|
|
||
|
|
|
|
|
|
||
|
|
||
|
|
|
|
Sum and Difference Formulas
Class 12 Math Chapter 2 Inverse Trigonometric Function Solution PDF: Free Download
We have compiled solutions for all exercises of Inverse Trigonometric Functions in one place for ease of students. Students can download the Class 12 Math Chapter 2 ITF solution PDF for free. The NCERT Solutions for Class 12 Maths Inverse Trigonometric Functions PDF is a very helpful document for all student boards as well as JEE Main, and other entrance exams. access the PDF below for free;
Class 12 Math Chapter 2 Inverse Trigonometric Function Solution: Free PDF Download
Class 12 Math Chapter 2 Inverse Trigonometric Function Exercise-wise Solutions
Inverse Trigonometric Function is an essential topic for building foundational trigonometric concepts. Chapter 2 Class 12 Math Inverse Trigonometric Function deals with the properties, domains, and ranges of inverse trigonometric functions. The ITF concepts also play a vital role in calculus, Matrices, Determinants, and other important physics and Math concepts and real-world applications. Students can check the exercise-wise Chapter 2 ITF math solutions below;
Class 12 Math Chapter 2 Inverse Trigonometric Function Exercise 2.1 Solutions
Chapter 2 Inverse Trigonometric Function Exercise 2.1 focuses on problems finding principal values, range, domain, and co-domain. Chapter 2 ITF Exercise 2.1 includes 14 Questions (12 Short Answers, 2 MCQs) primarily based on finding the values of inverse trigonometric functions. Students can check the complete the exercise 2.1 solutions below;
Inverse Trigonometric Function Exercise 2.1 Solutions
Find the principal values of the following:
Q1.
A.1. Let sin−1 =y. Then, sin y=-
We know that the range of principal value branch of sin−1 is
and sin−1
=
Principal value of sin−1
Q5.
A.5. Let cos -1
= cos
= cos
branch of cos−1 is [0,
Principal value of cos−1
Find the values of the following:
Q11.
A.11. tan−1(1) + cos−1
Q12.
A.12. cos−1
=
=
=
Q13.
A.13. Given, Sin−1x=y.
(E) We know that the principal value branch of Sin−1 is
Option B is correct.
Q14.
A.14.
=tan−1
=
=
=
Option B is correct.
Class 12 Math Chapter 2 Inverse Trigonometric Function Exercise 2.2 Solutions
Chapter 2 Inverse Trigonometric Function Exercise 2.2 consists of 21 Questions (18 Short Answers, 3 MCQs). Chapter 2 ITF contains questions related to solving ITF equations and finding the values of complex inverse trigonometric functions. Students can check the complete exercise 2.2 solutions below;
Relation and Function Exercise 2.2 Solutions
Q1.
A.1. We know that.
sin 3θ =3 sin θ 4sin3θ (identity).
(E) Let x = sinθ. Then, sin −1x=θ . We have,
Sin3(sin −1x) = 3x−4x3
3sin −1x =sin-1 (3x−4x3)
Hence proved.
Q2.
A.2. We know that,
cos3θ= 4cos3θ - 3cosθ
Letx = cosθ Then θ = cos-1x. We have,
Cos3(cos-1x) = 4x3-3x
3cos-1x = cos-1(4x3- 3x)
Hence Proved
Q3.
A.3. L.H.S = tan -1
Using tan -1x+ tan -1y= tan -1
L.H.S =tan -1
tan -1
Q4.
A.4. L.H.S= 2 tan -1
(E) Using2 tan -1x= tan -1
L.H.S = tan -1
= tan -1
= tan -1
= tan -1
= tan -1
= tan -1
Write the following functions in the simplest form:
= tan -1
tan -1
Q8.
A.8. Given tan -1
(M) Dividing numerator & denominator cos x we get,
tan -1
We know that
Find the values of each of the following:
Q11.
A.11.
(E)
Q12.
A.12. cot
(E)
Q13.
A.13.
(M) Let x = tanØ . then tan-1x= 0 and y = tan ω then tan-1y = ω. we have,
tan
=
Q14.
A.14.
(E)
= x =
Q15.
A.15.
(E)Using
Find the values of each of the expressions in Exercises 16 to 18.
Q16.
A.16.
(M) As
Q17.
A.17.
(M). As
=
Q18.
A.18.
(M) Let
Then
Hence, tan x =
Q19.
A.19. Cos-1 cos
(M) As
cos-1
= cos-1
=
So, option B is correct
Q20.
= sin
= sin
= sin
Class 12 Math Chapter 2 Inverse Trigonometric Functions Miscellaneous Exercise Solutions
The Miscellaneous Exercise of Inverse Trigonometric Function Chapter 2 Class 12 Maths contains 17 Questions (14 Short Answers, 3 MCQs). Students are provided with complete Miscellaneous Exercise solutions with detailed explanations including all the important concepts and more. The Chapter 2 ITF Miscellaneous Exercise consists of summarised examples of all the previous exercises. Students can complete Chapter 2 miscellaneous exercise well;
Inverse Trigonometric Function Miscellaneous Exercise Solutions
Find the value of the following:
Q1.
A.1. Cos-1
=
=
Q2.
A.2.
Q4.
A.4. Let
(N. then,
So,
Using.
tan
sin-1
Hence proved.
Q5.
A.5.
Let cos-1
Then,
Using
Q6.
A.6.
Let
Thin,
Using
Q7.
A.7. Let
Then,
So,
Using
tan
Hence proved.
Q8.
A.8. LH.S
=
Solve the following equations:
Q13.
A.13. Given,
Q14.
A.14. Given, (M)
Q16.
A.16.
(M) Let
Putting this in
Putting
L.H.S
So,
Option (c) is correct.
Q17.
A.17.
Option C is correct.
Class 12 Math important reference books and preparation Tips
All students preparing for competitive exams must have the right resource list before starting their preparation. Shiksha brings the list of the most recommended books for competitive exam maths preparation. Students with the right resources excel in both board and competitive exams such as JEE, COMEDK, etc... Candidates can check the preparation tips and book recommendations below;
Important Maths Reference Books For Preparation
- RD Sharma Mathematics for Class 12 ( ( Vol.I and II)
- Objective Mathematics by R.D. Sharma
- Cengage Mathematics Book Series by G. Tewani
- Problems in Calculus of One Variable by I.A. Maron
- Trigonometry and Co-ordinate Geometry by SL Loney
Students can also discuss other books available in the market for JEE Main preparation for Maths. Students must discuss the options with their teachers or mentors before buying the books.
Preparation Tips for Class 12 Math and JEE Main
- Know Your Exam: Go through the Exam pattern and syllabus of the targeted exam, and read thoroughly to get an idea of the examination method and the level & type of questions asked. Students should also read some of the previous year's papers for the exam before starting the preparation
- Pick the Right Preparation Resources: Take the help of seniors, teachers, and mentors while choosing the resources. Students must find resources which is crisp and concise and contain the same level of questions and examples as asked in the exam.
- Make a Preparation Plan: Students should make a realistic preparation plan which should include enough time for practice and revision of the already learned concepts and allow them to cover all the concepts within the exam deadline
- Practice: This step can be a key to success for students, students must practice more and more sums and numerals. Practice gives students an edge over computational errors, and critical thinking which helps boost confidence.
Revisions: Students should revise the concepts and important sum techniques multiple time to make them very handy so that those concepts and techniques can be used in real-time exam situations. - Solve Mock Test: Students should try to solve as many Mock test/ Board sample papers as possible. Students should attempt Chapter-wise, sectional and complete mock test as per the preparation condition and time.
Maths Ncert Solutions class 12th Exam