/ Preparation Maths Mensuration
- What is Mensuration?
- Weightage and Importance of Mensuration
- Illustrated example on Mensuration
- FAQs on Mensuration
What is Mensuration?
Mensuration is the measurement of geometric figures. This chapter will learn about some additional quadrilaterals, their areas, perimeter, surface areas, and volumes.
Trapezium:
A trapezium is outlined by a form that has 2 parallel sides, and the other 2 are nonparallel. It has four sides and four vertices.
| Shape |
Area |
Perimeter |
|---|---|---|
| 1. Trapezium |
Area= (1/2) H + (AB+CD) |
P= sum of all the sides i.e. AB+BC+CD+AD |
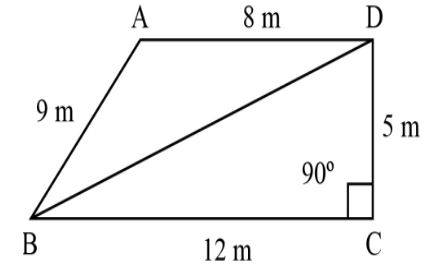
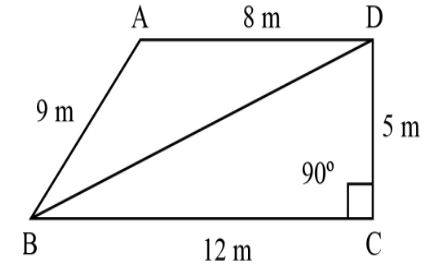
| 2. General quadrilateral |
Area= Area of △ABC + Area of △ADC |
The perimeter depends on the type of shape which is present |
| 3. Special quadrilateral (rhombus) |
½ × d1 × d2 |
P=4a |
Where, H= height, W= breadth, a,b,c,d= sides, d= diagonals
Quadrilateral
Surface area: The definition is that the total area of all the surfaces of any form.
Volume: the degree is outlined by the number any third-dimensional form takes.
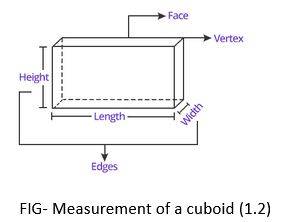
Solid shapes:
Solid shapes are measured by their three-dimensional structure with outlined breadth, height and length. A cube, sphere, cylinder, cuboid are solid shape examples.
| Shape |
Surface area |
Volume |
|---|---|---|
| 1. Cube |
Area= 6a^2 |
V= a^3 |
| 2. Cuboid |
Area= 2 [(l × b) + (l× h) + (b× h)] |
V= l*w*h |
| 3. Cylinder |
Ares= 2πr (r + h) |
V= πr2 × h |
Where, H= height, a= sides, r= radius, d= diameter, b= breadth, w= width
Weightage and Importance of Mensuration
The chapter Mensuration is in class 8. It is chapter 11 of NCERT textbook. The weightage is 15% of the total marks.
Illustrated example on Mensuration
1. Calculate the area of a rhombus whose diagonals 10 cm and 8.2 cm of length.
Solution:
The formula for calculating area of a rhombus = ½ d1d2, (d1 and d2 are the lengths of the diagonal)
a= 2 × 10 × 8.2 cm2 = 41 cm2.
2. A rhombus with an area of 240cm2 and whose one diagonal is of length 16 cm. Find the other diagonal.
Solution:
We know d1 = 16 cm and let the other diagonal = d2
Thus the area of the rhombus = 2 d1 . d2 = 240,
So, ½ 16 d2 = 240
Therefore, d2= 30cm.
Diagonal 2 is 30 cm.
3. A cuboid-shaped aquarium is a present whose external measurements are of 80 cm × 30 cm × 40 cm. The base, side faces and back face are to be covered with a coloured paper. Find the area of the paper needed?
Solution: The length of the aquarium = l = 80 cm
Width of the aquarium (b) = 30 cm
Height of the aquarium (h) = 40 cm
Thus the area of the base = 80 × 30 = 2400 cm2 ,
Area of the side face = 30 × 40 = 1200 cm2 &
Area of the back face = 80 × 40 = 3200 cm2
Thus area required to be calculated = Area of the base + area of the back face + (2 × area of a side face)
= 2400 + 3200 + (2 × 1200) = 8000 cm2
FAQs on Mensuration
Q: What is the formula of the area of a cube?
Area=6a^2
Where a= sides of the cube
Q: What is the area of the quadrilateral?
Example: area of general quadrilateral= space of △ABC + Area of △ADC
Q: What is the height of a cylindrical structure?
Q: How many edges and faces will a cuboid have?
Q: What is the area of a cuboid?
Where, l= length, h=height, b= breadth
Maths Mensuration Exam
Student Forum
Anything you would want to ask experts?Answered 2 weeks ago
CLAT does not publish a fixed number for this topic. It is tested within the wider Quantitative Techniques section, so the count changes by year and paper.
S
Contributor-Level 10
Answered 2 weeks ago
Learn all basic formulas. Practise unit conversion daily. Draw quick diagrams for composite figures. Revise common traps often to build speed and accuracy.
S
Contributor-Level 10
Answered 2 weeks ago
There is no single fixed book. Most students use standard Class 10 maths books. They combine this with CLAT-specific practice sets and previous year papers.
S
Contributor-Level 10
Answered 2 weeks ago
Start early, along with other Quantitative Techniques topics. Strong basics in formulas make composite and caselet questions much easier later on.
S
Contributor-Level 10
Answered 2 weeks ago
Mensuration is part of the Quantitative Techniques syllabus. Questions from this topic show up regularly in past papers. Skipping it means fewer scoring chances in an already short section.
S
Contributor-Level 10
Answered a month ago
Yes, Mensuration is an important topic for CAT Quantitative Aptitude. If forms a good chunk of Geometry questions.
M
Contributor-Level 7
Answered a month ago
About 2-4 questions can be asked from Mensuration section in CAT. Candidates can must practice this topic extensively.
P
Contributor-Level 7
Other Class 10th Maths Chapters
Popular Courses After 12th
Exams accepted
CA FoundationExams accepted
ICSI ExamExams accepted
BHU UET | GLAET | GD Goenka TestBachelor of Business Administration & Bachelor of Law
Exams accepted
CLAT | LSAT India | AIBEExams accepted
IPMAT | NMIMS - NPAT | SET
Exams accepted
BHU UET | KUK Entrance Exam | JMI Entrance ExamBachelor of Design in Animation (BDes)
Exams accepted
UCEED | NIFT Entrance Exam | NID Entrance ExamBA LLB (Bachelor of Arts + Bachelor of Laws)
Exams accepted
CLAT | AILET | LSAT IndiaBachelor of Journalism & Mass Communication (BJMC)
Exams accepted
LUACMAT | SRMHCAT | GD Goenka Test
How many questions are asked from Mensuration in CLAT?