Rachit Kumar SaxenaManager-Editorial
What are Cube and Cuboids?
Cubes and cuboids are basic 3-dimensional shapes that have six faces, eight vertices, and twelve edges. However, Cubes have all sides of the same length; they’re the 3D extension of a square and cuboids have different sides. Hence, their areas and volumes also differ. The angles of a cube and cuboid are right angles.
Properties of a Cube
- The sides are all equal.
- The faces are squares of equal areas.
- All diagonals from any two points of the cube are equal.
Properties of a Cuboid
The dimensions are unequal.
The faces of the cuboid are different rectangles. Any two non-opposite faces are called adjacent faces.
Only the opposite and parallel diagonals are equal in a cuboid.
Formulae of Cube and Cuboid
| Cube (of side a) |
Cuboid (of dimensions l, b and h) |
|---|---|
| Total Surface Area = 6a2 |
Total Surface Area = 2 ( lb + bh + lh ) |
| Lateral Surface Area = 4a2 |
Lateral Surface Area = 2h ( l x b) |
| Volume = a3 |
Volume = l x b x h |
| Diagonal = 3a |
Diagonal = (l2 + b2 + h2) |
| Perimeter = 12a |
Perimeter = 4( l + b + h) |
Difference between Cube and Cuboid
Though both cube and cuboid are three-dimensional figures, they have some dissimilarities between them. The faces of a cube are square-shaped, whereas a cuboid has rectangular faces. This is the basic difference between them. The other differences are described below.
Cube
Cube is a 3D-figure that has eight vertices, six faces, and twelve edges. Each of its faces is square in shape, and each of the edges and shapes has an angle that measures 90-degrees between them. The below image shows the pictorial depiction of a cube:
Cuboid
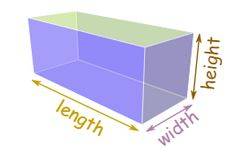
Cuboid is a 3D-figure that also has eight vertices, twelve edges, and six faces. Unlike a cube that has all square faces, a cuboid might have rectangular faces or the faces might have different dimensions as well. The below image shows the pictorial depiction of a cuboid:
Cube v/s Cuboid
The comparison table of cube and cuboid on the basis of various features is given below:
| Differentiating features |
Cube |
Cuboid |
|---|---|---|
| Shape |
3-dimensional form of a square (example - Rubik’s Cube) |
3-dimensional form of a rectangle (example - Brick) |
| Diagonals |
12 (each diagonal is of the same length) |
12 (3 sets of diagonals are of the same length) |
| Internal Diagonals |
4 (all are of same length) |
4 (2 are of same length) |
| Lateral Surface Area |
4 x side x side |
2 (sum of length and breadth) x height |
| Total Surface Area |
6 x side x side |
2 [(product of length and breadth) + (product of breadth and height) + (product of length and height)] |
| Diagonal of Cube |
√3 x side |
√length x length + breadth x breadth + height x height |
| Volume |
side x side x side |
length x breadth x height |
| Perimeter |
12 x side |
4 x length x breadth x height |
Weightage of the Topic
Students are introduced to 3D shapes like the cube and cuboid a Class 7 and 8. In Class 9 to 10, they are given problems regarding measuring the dimensions of these two shapes. These concepts help them to analyse and calculate real-life applications of these shapes. Industries also use this to calculate costs and dimensions in engineering and architecture.
The topics related to volume, surface area, and other aspects of cube and cuboid are covered in Class VIII’s chapter ‘Mensuration’. This chapter has a weightage of 15 marks, which means that questions ranging from 4 to 6 marks can be asked on this particular topic.
Illustrative Examples on Cube and Cuboid
1. An aquarium is a cuboid whose external measures are 80 cm × 30 cm × 40 cm. The base, side faces, and back face are to be covered with a coloured paper. Find the area of the paper needed?
Solution.
l = 80, b = 30, h = 40
The area of paper needed = (area of the two side faces) + (area of the back face) + (area of the base)
= 2400 + 3200 + (2 × 1200) = 8000 cm2
2. The internal measures of a cuboidal room are 12 m × 8 m × 4 m. Find the total cost of whitewashing all four walls of a room, if the price of whitewashing is Rs 5 per m2. What will be the cost of whitewashing if the ceiling of the room is also whitewashed?
Solution.
l= 12, b= 8 and h = 4.
Area of the four walls of the room = Perimeter of the base × Height of the room
= 2 (l + b) × h = 2 (12 + 8) × 4
= 2 × 20 × 4 = 160 m2
Cost of white washing per m2 = Rs 5
Total cost of white washing the room = Rs (160 × 5) = Rs 800
Area of ceiling is 12 × 8 = 96 m2
Cost of white washing the ceiling = Rs (96 × 5) = Rs 480
So, the total cost of white washing = Rs (800 + 480) = Rs 1280
3. Two cubes of volume 8cm3 are placed together to obtain a rectangle. What is the perimeter of the rectangle?
Solution.
Volume of cube = 8 cm3, hence side of the cube = 38 = 2 cm3
The length of the rectangle formed is 2 + 2= 4 cm.
The breadth of the rectangle is 2 cm.
Hence, perimeter of the rectangle = 2(l +b) = 2( 4 + 2)= 12 cm
4. The side of a cube is equal to 6cm. Find its total surface area and the length of its diagonal.
Solution.
The total surface area of a cube = 6 x side x side = 6 x 6 x 6 = 216 square cm.
The length of a cube’s diagonal = √3 x side = √3 x 6 = 10.39 square cm.
5. A cuboid’s length, breadth, and height are 2, 4, and 8cm respectively. Find its volume and total surface area.
Solution.
Volume of a cuboid = length x breadth x height = 2 x 4 x 8 = 64 square cm.
Total surface area of a cuboid = 2 [(product of length and breadth) + (product of breadth and height) + (product of length and height)]
= 2 [(2 x4) + (4x8) + (2x8)] = 2 [8 + 32 + 16] = 2 x 56 = 112 square cm.
6. Find the perimeter of a cube if its side measures 4cm.
Solution.
Perimeter of a cube = 12 x side = 12 x 4 = 48 cm
FAQs on Cube and Cuboid
Q: Is a cube a type of cuboid?
Q: What are the formulae for diagonal for cube and cuboid?
Diagonal =(l2 + b2 + h2)
Q: Are all the diagonals in a cuboid equal?
Q: Why are all the sides of a cube equal?
Q: How to calculate perimeters of a cube and cuboid?
Perimeter of a cuboid = 4( l + b+ h)
Q: Can a cube be referred to as a cuboid?
Q: What is the longest rod in a cuboid?
Q: What are the other names of a cuboid?
Q: How many right-angled triangles can fit inside a cube?
Q: Give other names for a cube?
News & Updates
Maths Mensuration Exam
Student Forum
Popular Courses After 12th
Exams: BHU UET | KUK Entrance Exam | JMI Entrance Exam
Bachelor of Design in Animation (BDes)
Exams: UCEED | NIFT Entrance Exam | NID Entrance Exam
BA LLB (Bachelor of Arts + Bachelor of Laws)
Exams: CLAT | AILET | LSAT India
Bachelor of Journalism & Mass Communication (BJMC)
Exams: LUACMAT | SRMHCAT | GD Goenka Test