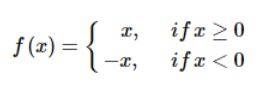Rachit Kumar SaxenaManager-Editorial
What is Modulus Function?
A modulus function is a function that takes an absolute value; for example, a number becomes greater or smaller. It defines the true extent of the sum of variables. The average is also regarded as an absolute value function. The product of this function will always equal a positive value, regardless of the data. It is seen as y=|x|. The plotting of such graphs is also a simple approach where the scope will be all values of input say x (all real numbers) and range will be all values of function (y = f(x) = all positive real numbers and 0).
Modulus Function Definition
A relation "f" is called a function if it maps each element of an initial segment of the universe to a single element in a series. The function f(x) of x is known as:
f(x) = |x|.
Or
y = |x|.
Where f: R→R and x belongs to R.
And |x| denotes the number mod x.
If x is positive, then only x will be produced by the function f(x). If x is negative, so the magnitude of x is what x is. Therefore, we should redefine the modulus function as follows:
Modulus Function Graph
Now, let us plot a graph for modulus function. Let x denote a variable whose values range from negative three to positive three, the domain of the graph. The graph should always be a continuous function of x at each value, as per the concept. Consider the table given where the y-axis shows the value of y and the x-axis shows the value of x; then we can plot the graph.
The graph indicates that the values of the modulus function remain positive for all the values of the variable, such as; x
When x = -3 then y = |-3| = 3
When x = -2 then y = |-2| = 2
When x = -1 then y = |-1| = 0
When x = 0 then y = |0| = 0
When x = 1 then y = |1| = 1
When x = 2 then y = |2| = 2
When x = 3 then y = |3| = 3
Weightage of Modulus Function in Class 11
This concept is taught under the chapter Relations and Functions. You will learn about the basics of this function and its uses. The weightage of this chapter is 6 marks in your final exam.
Illustrated Examples of Modulus Function
1. Solve modulus and find the interval of b for |b^2 – 5b + 6|
Solution:
|b^2 – 5b + 6| = |(b – 2)(b – 3)| = |f(b)|
As per modulus definition,
|f(b)| = f(b); if f(b) is positive
| f(b) |= -f(b); if f(b) is negative
f(b) = (b – 2)(b – 3) is positive or zero when b = (- ∞, 2] ∪ [3, ∞)
f(b) = (b – 2)(b – 3) is negative when b = (2, 3)
So, |b^2 – 5b + 6| = (b^2 – 5b + 6) when b = (-∞, 2] ∪ [3, ∞) and
|b^2 – 5b + 6| = -(b^2 – 5b + 6) when b = (2, 3)
2. Locate the domain and range of the feature below?
Y = |1−x|
Solution:
Y = |1 ‒ x|
Obviously, this is known as x x R. Then it's Domain R.
Right now |1 − x| ≥ 0 for all x ∈ R
So the range [0, ∞ )
3.Locate the domain and range of the feature below?
Y = 2 − |1 ‒ x|
Solution:
Y = 2 − |1 ‒ x|
Obviously, this is known as x x R. Then it's Domain R.
Right now |1 − x| ≥ 0 for all x ∈ R
or
−|1 − x| ≤ 0 ≤ 0
2 − |1 − x| ≤ 2 for all x'R's
Then the range is (−∞, 2]
FAQs on Modulus Function
Q: What does the modulus equation mean?
Q: What is the concept of modulus?
Q: What's the use of modulus in everyday life?
Q: What is the coding modulus?
Q: Is modulus function onto?
News & Updates
Maths Relations and Functions Exam
Student Forum
Popular Courses After 12th
Exams: BHU UET | KUK Entrance Exam | JMI Entrance Exam
Bachelor of Design in Animation (BDes)
Exams: UCEED | NIFT Entrance Exam | NID Entrance Exam
BA LLB (Bachelor of Arts + Bachelor of Laws)
Exams: CLAT | AILET | LSAT India
Bachelor of Journalism & Mass Communication (BJMC)
Exams: LUACMAT | SRMHCAT | GD Goenka Test