Rachit Kumar SaxenaManager-Editorial
What is One-to-one Function?
Functions are extremely significant in mathematics. Thus, it is essential to understand the basics of a function before forging ahead with a one-to-one function. The function states that for every x there is a y. It arises when one element from one set is dependent on exactly one element from another set.
You must understand the one-to-one function to understand any form of equation surrounding the concept of the inverse function and its characteristics. In case of the 1-1 function, here is only one x can be combined with a given y.
What is a One-one Function?
A function is considered a one-to-one function if no two different elements in one set have the same element in another set. The function f(x) can be a one-to-one function only if each element in its spectrum is returned from its domain by a single element. This implies there would be a special value of y for any value of x.
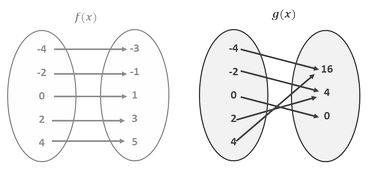
Here, in this example, you can see that the function f(x) is a 1-1 function as every element from one set has a unique element in another set unlike g(x) where two elements from one set have a common function in another set. Therefore, the function g(x) is not a one-one function.
Graph of a One-one Function
The graph of 1-1 function is required to comprehend the concept of one-one function fully. There is a special value of y for any value of x. Therefore, each x is expected to have a unique value for y in a one-one function. No pairs of elements in the x-axis will share coordinates with another element in the y-axis. The graph below will deliver better insights regarding the concept of one-one function.
The above graph accounts for a one-one function where two elements on the x-coordinate are having two distinct elements in the y-coordinate without any sharing taking place among them.
Weightage of one-to-one functions in Class 12
The topic of one-to-one functions is from the chapter relations and functions. The chapter includes various other topics such as types of relations. The chapter has a weightage of eight marks in the 12th final examination.
Illustrative examples on One-to-one Function
1. Show that f is one – one for the following set, Let C = {1, 2, 3} D, = {4, 5, 6, 7} and let f = {(1, 4), (2, 5), (3, 6)} be a function from C to D.
Solution.
f: C → D can be shown as f = {(1, 4), (2, 5), (3, 6)}
We can figure out that each element of A under is unique. Thus, function f is one-one.
2. Show how f is one-one onto where f: R → R can be expressed as f(x) = 3x.
Solution.
Given, R → R can be expressed as f(x) = 3x
Let us consider x and y as the element of R
Therefore, f(x) = f(y)
3x = 3y
x = y, f is one-one.
We can also consider y/3 in R for any real number (y) in the co-domain R. Therefore, f is onto.
3. Show how f is one – one onto where f: R → R can be expressed as f(x) = 2x+1.
Solution.
Given, R → R can be expressed as f(x) = 2x+1
Let us consider x and y as the element of R
Therefore, f(x) = f(y)
2x+1 = 2y+1
x = y, f is one-one.
We can also consider y/3 in R for any real number (y) in the co-domain R. Therefore, f is onto.
FAQs on one-to-one functions
Q: Which graph depicts a one-one function?
Q: What is not considered to be a one-one function?
Q: What is the other name of a one-one function?
Q: Can we consider parabola as a one-one function?
Q: Give some viable examples of one to one function.
News & Updates
Maths Relations and Functions Exam
Student Forum
Popular Courses After 12th
Exams: BHU UET | KUK Entrance Exam | JMI Entrance Exam
Bachelor of Design in Animation (BDes)
Exams: UCEED | NIFT Entrance Exam | NID Entrance Exam
BA LLB (Bachelor of Arts + Bachelor of Laws)
Exams: CLAT | AILET | LSAT India
Bachelor of Journalism & Mass Communication (BJMC)
Exams: LUACMAT | SRMHCAT | GD Goenka Test