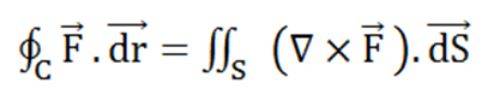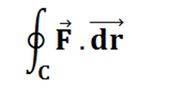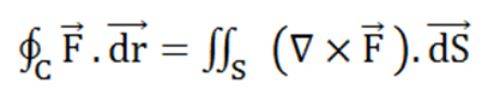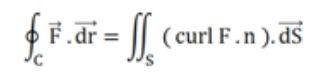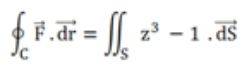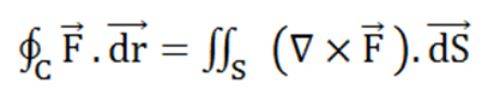Stokes Theorem: Overview, Questions, Preparation

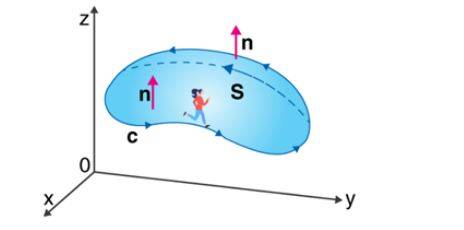
Stoke's Theorem is an important theorem that shows the relationship between a line and a surface integral of vector fields. It mainly states that the surface integral of a function's curl over a surface bounded by a closed surface is always equal to the line integral of the particular vector function around that surface.

Formula:

The formula for Stoke's Theorem is:

Here, 
C indicates a closed curve.
S indicates any surface surrounded by C.
F is a vector field whose components have constant derivatives in R3's open region containing S.

Stoke's theorem is an essential topic of chapter Vector Algebra. Chapter Vector Algebra if present in class XII. Vector Algebra is a necessary topic as per the class XII examinations and the other competitive exams. The chapter's weightage in class XII examinations ranges from 7 to 10 marks. And 3 to 5 questions having moderate to difficulty level are always asked in class XII exams.

The importance of the topic stoke's theorem is majorly present in higher studies and other competitive exams. Stoke's theorem mainly uses applications of vectors and calculus. In the chapter of Vector Algebra, other topics are also present, such as:

• Various kinds of Vectors
• Addition of similar or different Vectors
• Multiplication of a Scalar and Vector
• Product of two same or different vectors

1. Compute 

where F = y i + xz³ j - zy³ k. And C is the circle oriented in an anti-clockwise manner and is present in the plane z = -3, x²+y² ≤ 4.

Solution. 

We know the formula for stoke's theorem is 

it can also be written as

where n is the normal vector,

The value for curl(F)* n = [d(xz3)/dx - d(y)/dy] = z3 -1,
z = -3 (given), therefore z3 -1 = -27 - 1 = -28
Now,

2. Prove that the line integral ∮C yz.dx + xz.dy + xy.dz is 0 along the closed surface C.
Solution. 

For a closed surface C let S be its bounded surface. 

As per the Stoke's formula, we can see that P = yz, Q = xz, R = xy.

Therefore,

 ∇×F = (dR/dy - dQ/dz) i + (dP/dz - dR/dz) j + (dQ/dz - dP/dy) k, 

After solving this we will get 0 i + 0 j + 0 k = 0.

Hence putting the value of ∇×F into the Stoke's formula,

we will get zero. 
Hence by this, it is proved that the line integral for the statement is zero.

3.What will happen if a Sphere has no boundary?
Solution. 

If a sphere does not have any boundary present, then the line integral across the object's boundary will be zero.

Q: Write the Stoke's Theorem in the coordinate form.

A:

Q: Which operation is used in Stoke's Theorem?

Q: Mention the primary difference between Stoke's Theorem and Green's Theorem.

Q: When was Stoke's theorem invented?

Q: How can we use Stoke's theorem?