Biot-Savart Law: Class 12 Physics Notes, Definition, Formula, Applications, & Examples

We know that all magnetic fields are because of moving charges or currents and intrinsic magnetic moments of particles. Biot-Savart's law establishes the relation between the current and the magnetic field it produces

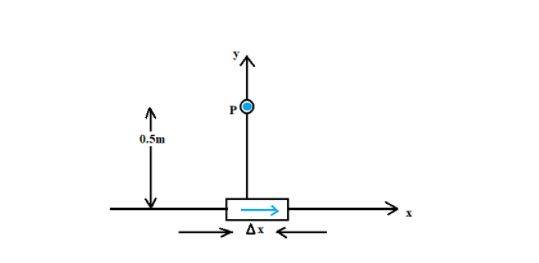
Diagrammatic Explanation of Bio-Savart Law

 

(Image Source: NCERT eBook)

We have a conductor named XY carrying current I. Considering a minuscule element dl of the conductor, we have to find the magnetic field dB resulted by this element at a point p at a distance r from it. Assume Θ is the angle between dl and displacement vector r. Biot-Savart law says that the magnetic field dB size is directly proportional to the current I and the element length |dl|, and inversely proportional to the square of the distance r. Its direction is perpendicular to the plane of dl and r.

dB ∝ (Idl) x r/r³

 = µ0/4π x (Idl) x r/r³

where µ0/4π is the proportionality constant. The above equation works only when the medium is the vacuum.

The magnitude of the magnetic field is

$\begin{array}{l}\left|dB\right|=(\frac{{\mu }_0}{4\pi })(\frac{Idssin\theta }{r^2})\end{array}$

The constant of proportionality µ0/4π has the value 10-7 Tm/A. µ0 is the permeability of free space.

The application of Biot-Savart law is mentioned below.

• Calculate the magnetic field in centre of a current-carrying arc, and indefinitely long straight wire owing to a constant current
• Calculate forces between lengthy and parallel current-carrying conductors. 

The topic 'Biot-Savart Law' is covered in the chapter 'Moving charges and Magnetism' of the third unit of class XII NCERT Physics. The other chapter is 'Magnetism and matter'. The fourth unit comprises the chapters 'Electromagnetic Induction' and 'Alternating Current'. These two units are combined in the exams for a total of 17 marks.

Example 1: An element dl = Δx is placed at origin and carries a current I = 10A. Find the magnetic field on the y-axis at a distance of 0.5m. Δx = 1cm.

Solution:  

|dB| = µ0/4π x (IdlsinΘ)/r²

dl = Δx = 10-²m, I = 10A, r = 0.5, m = y, µ0/4π = 10-7 Tm/A.

Θ = 90°; sinΘ = 1.

|dB| = (10-7x10x10-²)/(25x10-²)=4x10-8T

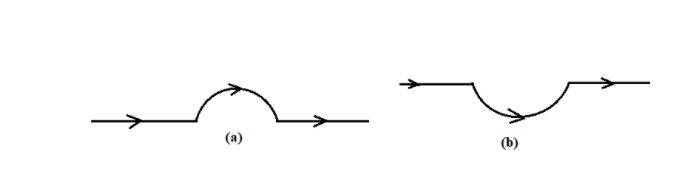
Example 2: A straight wire carrying 12A is bent into a semi-circular arc of radius 2cm. Considering the magnetic field B at the centre of the arc,

1. a) calculate the magnetic field due to straight segments
2. b) In which way does the contribution of B in the semi-circular arc differ from that of a circular loop?
3. c) What if the semi-circular arc of the same radius was bent in the opposite direction as shown in the second figure? 

Solution: a) dl and r for each element of the straight segments are parallel.

Therefore, dl x r = 0.

Thus straight segments do not contribute to |B|.

1. b) For all segments of the semi-circular arc, dl x r are parallel to each other.  All such add up in magnitude. The right-hand rule gives the direction of magnetic field B, and its magnitude is half that of a circular loop.

B = 1.9x10-4T.

1. c) The same magnitude of B as that in b) but in the opposite direction.

Example 3: Consider a 100 turn coil of radius 10cm carrying a current of 1A. Find the magnitude of the magnetic field?

Solution: Given, radius R = 10cm = 0.1m

                        Number of turns N = 100

                        Current I = 1A

Thus,

B = µ0NI/2R 

    = 4πx10-7x10²x1/(0.2) 

    = 2πx10-4 

    = 6.28x10-4.

Q: What is Biot-Savart Law?

Q: Write the Biot-Savart law equation.

Q: What is µ0?

Q: What is the condition for which Biot-Savart law holds?

Q: What is µ0/4π?