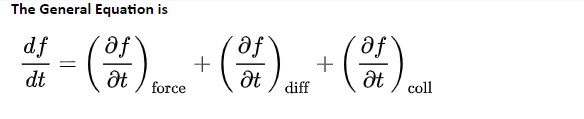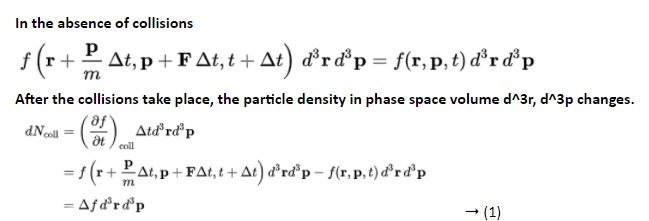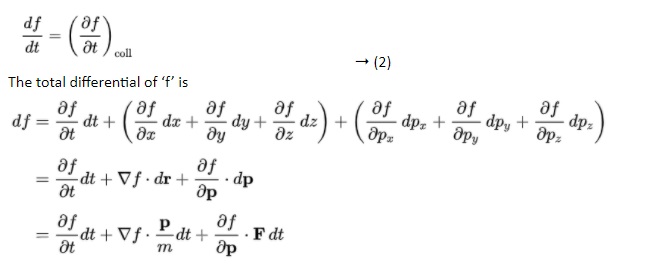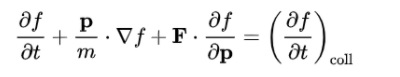Boltzmann Equation: Overview, Questions, Preparation

If we take a hot, dense gas, the large numbers of atoms collide with each other, leading to the excitation to the various energy levels. After some time scales, molecules exhibit radiative de-excitation. At constant temperature and pressure, equilibrium built between the collisional excitations and radiative deexcitations. 

• The equilibrium leads to the distribution of atoms between the energy levels. At higher temperatures, the large number of atoms occupy at high energy levels.
• Thus the Boltzmann equation shows the distribution of atoms among different energy levels as a function of energy and temperature.

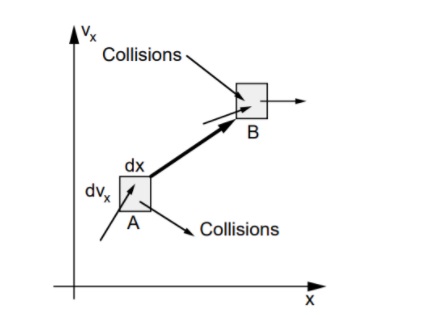
The Boltzmann equation helps us to define the properties of dilute gases. It analyses the elementary collision processes between a pair of molecules. In general, the Boltzmann equation is expressed as a kinetic equation that describes the change of macroscopic quantity in a thermodynamic system, such as energy, charge or particle number.

• A plasma is an ensemble of particles electrons ‘e,’ ions ‘i’ and neutrals ‘n’ with different positions ‘r’ and velocities ‘v,’ which move under the influence of external forces (electromagnetic fields, gravity) and internal collision processes (ionisation, Coulomb, charge exchange) 
• The macroscopic plasma parameters are j - current density, ne - electron density, P - pressure, and Ti - ion temperature.

Explanation

• Consider particles as f, each particle experiences an external force F. The distribution of particles is dependent on the time t, position r and velocity v. At time t, the number of particles all has position r within an element d^3r and momentum p within d^3p.
• If a force F acts on each particle, at time t +Δt, their position is r+Δr = r+pΔtlm and momentum p+Δp = p+FΔt.

Δf = total change in f and the above equation when divided by  d^3r, d^3p Δt and taking the limits Δt➝0, Δf➝0, we get

➝ (3)

Where⛛ is gradient operator and • is the dot product.

Further dividing equation 3 by dt and substituting in eq 2 gives,

The equation simply states that df/dt = 0 unless there are collisions.

In chapter ‘Thermodynamics,’ the Boltzmann equation has less probability than other thermodynamics laws. The Boltzmann equation is an elaborated topic with different applications in physics. The weightage of this topic is below 5 marks.

Q: What are the applications of the Boltzmann equation?

Q: What is the Maxwell-Boltzmann distribution?

Q: What is the Collisionless Boltzmann Equation?

Q: What is the convective derivative?

Q: What is the Boltzmann Planck equation?

Q: What are the macroscopic variables?