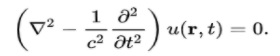Introduction
Helmholtz equation or reduced wave equation is a significant linear partial differential equation. It has many applications in the fields of physics and mathematics. It takes the name from the German physicist Hermann von Helmholtz.
Properties of Helmholtz Equation
- The equation involves an operator, ⛛2, which is called the Laplacian, also written ⛛⋅⛛.
- In mathematics, the eigenvalue problem for the Laplace operator is the Helmholtz equation.
- Where A is Amplitude and K is the wavenumber. K is real or constant, but it can be complex if the medium of propagation is energy-absorbing, or a function of space if the medium is inhomogeneous.
- The equation also has the property of being linear.
- The equation arises when you look for mono-frequency or time-harmonic solutions to the wave equation.
- Time-harmonic waves are of fundamental importance in applications as diverse as noise scattering, radar and sonar technology and seismology.
Derivation of Helmholtz Equation
It is a time-independent form of the wave equation. The equation is an outcome on applying the separation of variables method. It is usually determined to reduce the complexity of the analysis.
The wave equation is given by
Now, the separation of variables begins by considering the wave function u(r, t).
Let us substitute the above form in the wave equation and carry out a simplification to get the following equation:
Applications of Helmholtz Equation
- One of the applications is to study the waveguides. Waveguides are devices that transmit acoustic or electromagnetic energy, but they typically do so only at a fixed discrete frequency.
- Some examples of where this equation is applicable are vibrating membranes(drums), lasers, propagating sound waves and earthquakes.
- One of the well known Quantum Mechanics related to Schrödinger’s equation is an extension of the Helmholtz equation.
- The Laplace equation is often used in electrostatics. On a more meta-level, the underlying similarity in the solutions helps us see the symmetry of nature.
Helmholtz Equation for Class 11
This topic ‘Helmholtz equation’ has its importance among the other topics of thermodynamics. It is applicable for both physics and mathematical problems. For this level, the derivation and applications of the Helmholtz equation are sufficient. In higher levels, you get to know about the three-dimensional Helmholtz equation and solutions to solve.
FAQs on Helmholtz Equation
Q: What is the Gibbs Helmholtz equation?
Q: What are the four thermodynamic potentials?
Q: What are the formulas for Helmholtz free energy and Gibbs free energy?
Q: What is the wave equation?
Q: What does the Laplacian operator do?
News & Updates
Physics Thermodynamics Exam
Student Forum
Popular Courses After 12th
Exams: BHU UET | KUK Entrance Exam | JMI Entrance Exam
Bachelor of Design in Animation (BDes)
Exams: UCEED | NIFT Entrance Exam | NID Entrance Exam
BA LLB (Bachelor of Arts + Bachelor of Laws)
Exams: CLAT | AILET | LSAT India
Bachelor of Journalism & Mass Communication (BJMC)
Exams: LUACMAT | SRMHCAT | GD Goenka Test