Rachit Kumar SaxenaManager-Editorial
What are Relations and Functions?
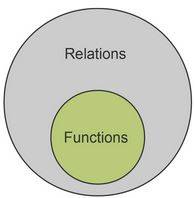
In algebra, relations and functions play the most crucial part. All functions are relations, but not all relations are functions. The relation between the two sets is formed by the Cartesian product of the subsets.
Relations
When two or more sets are connected through different means, it is termed as a relation. Consider ‘A’ and ‘B’ as two sets, and ‘x’ and ‘y’ are objects in it. So, we can say ‘A’, ‘B’ is in a relation if the objects ‘x’ and ‘y’ are connected by any means.
Different types of Relations
Universal relation- When all the objects in ‘A’ are related to the objects in ‘B’.
Empty relation- When none of the objects in ‘A’ is related to the objects in ‘B’.
Inverse relation- When the relation, R between ‘A’ and ‘B’ is equal to the relation, R-1.
Identity relation- When all the objects in ‘A’ are related to itself.
Symmetric relation- When all the objects in ‘A’, and ‘B’ are symmetrically identical.
Reflexive relation- When all the objects in set ‘A’ mirror themselves, it is known as reflexive relation.
Transitive relation- If set ‘A’ is equal to ‘B’ and set ‘B’ is equal to ‘C’, then set ‘A’ is equal to ‘C’.
Equivalence relation- When a relation is a combination of symmetric, transitive, and reflexive.
Functions
When there is an output for every input, then the relation is termed as a function. When all the objects of both the sets are related to each other, and an output is involved, it is termed as a function.
Different types of functions
One to one- When there is a distinct value in set ‘B’ for every value in ‘A’.
Many to one- When more than one object in set ‘A’ is related to one object in ‘B’.
Onto function- When for every element in set ‘B’ there is a preimage in ‘A’.
One-one to unto- When a function has all the elements of one to one and onto.
Difference between Relation and Functions
When two or more sets are connected through different means, it is termed as a relation. When there is an output for every input, then the relation is termed a function.
A relation is denoted by ‘R,’ and a function is represented by ‘f’ or ‘F’.
Every function is a relation, but not every relation is a function.
Weightage of Relation and Function in Class XII
The chapter ‘Relations and Functions’ would discuss different functions, relations, the composition of functions, binary operations, and invertible functions in detail.
Illustrative examples on Relations and Functions
1. For an arbitrary binary operation * on a set N, a*a = a ∀ a ∈ N. Is it true or false?
Solution. False
2. Consider a binary operation * on N defined as a*b = a3 + b3. Choose the right option.
a. Is * both associative and commutative
b. Is * associative but not commutative
c. Is * commutative but not associative
d. Is * Neither.
Solution. (b)
3. Is * defined on the set {1, 2, 3, 4, 5} by a*b = L.C.M. of ‘a’ and ‘b’ binary operation? Justify.
Solution.
Let a= 2 and b =3, considering the above-given equation.
a*b= 2*3= 6
Since 6 is not in the set, it is not a binary operation.
FAQs on Relation and Functions
Q: What is a relation?
Q: What are the types of relations?
Q: What is a function?
Q: What are the types of functions?
Q: State the difference between a relation and a function?
News & Updates
Maths Relations and Functions Exam
Student Forum
Popular Courses After 12th
Exams: BHU UET | KUK Entrance Exam | JMI Entrance Exam
Bachelor of Design in Animation (BDes)
Exams: UCEED | NIFT Entrance Exam | NID Entrance Exam
BA LLB (Bachelor of Arts + Bachelor of Laws)
Exams: CLAT | AILET | LSAT India
Bachelor of Journalism & Mass Communication (BJMC)
Exams: LUACMAT | SRMHCAT | GD Goenka Test