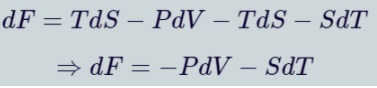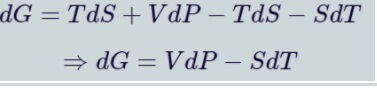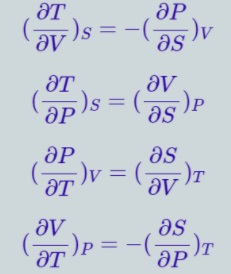Maxwell Relations: Overview, Questions, Preparation

In thermodynamics, we will have about 8 thermodynamic variables which could all be related to each by some function. Till now you have been familiar about the laws of thermodynamics, Enthalpy, Entropy, Gibbs free energy and Helmholtz Free Energy. Now, let’s move on to learn Maxwell’s relations of thermodynamic potentials.

A thermodynamic potential is a quantity used to represent the state of a system. We will consider four thermodynamic potentials for generating Maxwell relations

The internal energy (U) of a system is the energy contained in it due to motion and interaction of particles that exclude the energy outside of the system(due to external forces).

For the Hydrostatic system, the combined first and second law of thermodynamics gives a differential equation. Here, the entropy S and Volume V are the Natural variables.

Enthalpy(H)  is a thermodynamic potential which is equal to the internal energy of the system plus the product of pressure and volume. Here, the entropy S and pressure P are the Natural variables. The differential form of enthalpy is given by: 

Helmholtz free energy(H) of a system is equal to the internal energy of the system minus the product of its entropy and temperature. Volume V and temperature T are the Natural variables. The differential form of Helmholtz free energy is:

Gibbs free energy(G) used to calculate the amount of work a system performs at constant temperature and pressure. The Natural variables are pressure P and temperature T. The differential form of Gibbs free energy is

Maxwell relations connect two derivatives of thermodynamic variables and emerge due to equivalence of potential second derivatives under a change of operation order.

F is thermodynamic potential, and X and Y are two of its natural independent variables. Maxwell Relations named after James Maxwell

• Here we discuss the mathematical properties of these functions and consequences of the relationship between thermodynamic potentials. It will allow us to connect quantities that are difficult for measurements like the entropy and chemical potential.
• All thermodynamic potentials have multiple independent variables. The derivatives of potentials involve other thermodynamic potentials. So here we get four Maxwell relations after differential functions of thermodynamic potentials of Internal energy, Gibbs Free energy, Helmholtz Free Energy and Enthalpy.

Summary Table

Maxwell Relations involve numerical based differential equations and exhibit relation between thermodynamic potentials. A detailed explanation of equations is unnecessary at this level. Questions will be on the definitions and derivation of Maxwell relations. The weightage of the topic is less than 5 marks.

A: Thermodynamic equations describe thermodynamic potentials in terms of Natural variables. Temperature, pressure, entropy and volume are the Natural variables for describing U, H, A, G.

Q: What is the thermodynamic square?

A: Thermodynamic square is defined to compute the derivative of any thermodynamic potential.

Q: What are intensive and extensive thermodynamic variables?

A: An extensive variable is dependent on the system size like mass or volume. A number of particles(moles) are an example of an extensive variable. Intensive variables depend on types of matter like pressure, temperature and density variables.

Q: What is the utility of Maxwell Relations?

A: They are useful to derive quantities which are not easily measurable. Maxwell relations change them into quantifiable forms. They are also used to derive relationships between heat capacities of systems.

Q: Can we define Maxwell relations for other thermodynamic potentials?

A: Yes, it is possible to define the relation for other physical quantities. If a system is affected by some magnetic field. In that case, the internal energy acts as a natural variable which will change the Maxwell relation.