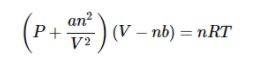Van Der Waals Equation: Overview, Questions, Preparation

The gaseous state of matter is the simplest form of matter. It has neither a fixed shape nor a fixed volume. It occupies the shape and volume of the container in which it is present. Gases have the following characteristics:

• They are highly compressible.
• Their intermolecular forces of attraction are almost negligible.
• They easily mix into each other, known as diffusion.
• They exert equal pressure in all directions.
• They have much lesser density than solids and liquids.

Based on his experiments, a scientist named Robert Boyle stated that the pressure of a fixed amount of gas at constant temperature varies inversely with its volume. Mathematically,

p∝1/V

or, p=k1 1/V, where k1=proportionality constant

or, pV=k1=constant.

Thus, p1V1=p2V2=constant.

Charles' law states that the volume of a fixed mass of a gas is directly proportional to its absolute temperature at constant pressure. 

V ∝ T

or, V=k2T, where k2=proportionality constant

or, V/T=k2=constant.

Thus, V1/T1=V2/T2=constant

Avogadro's law states that, at the same conditions of temperature and pressure, equal volumes of all gases contain an equal number of molecules. 

V∝n

or, V=k3n, where k3=proportionality constant.

The above three laws combine to give the ideal gas equation as follows:

V∝1/p (Boyle's Law)

V∝T (Charles' Law)

V∝n (Avogadro's Law)

Combining these equations, we get:

V∝nT/p

or, V=nRT/p.

Thus, pV=nRT.

This equation is called the ideal gas equation. R is the universal gas constant because it is constant for all gases.

We observe that the pressure exerted by any gas is lower than the pressure exerted by an ideal gas. Hence,

pideal = preal + an2/v2

where preal is the observed pressure and an2/V2 is the correction term.

Due to the change in pressure, the gas molecules are now restricted to volume (V-nb). nb is approximately the volume occupied by the molecules. b is a constant. Having taken these corrections into account, we can now write the ideal gas equation as:

This equation is known as the Van der Waals Equation. In this equation, n is the number of moles of the gas. a and b are Van der Waals constants whose value depends on the characteristic of the gas. 

Volume Correction

• In gas, molecules are considered as impenetrable spheres. So the available space for movement of molecules becomes less. 
• Let us assume the space available for 1-mole gas molecules Vi = (V-b)
• V - molar volume of the gas, b - volume correction factor, Vi - molar volume of the ideal gas, r - radius of the molecule and σ = 2r is the diameter.
• So the equation becomes Pi(V-b) =RT

When two molecules encounter each other, the distance between the centres of the molecules is σ. The excluded volume for a pair of molecules is (4/3)π r^3. 

For single-molecule = 1/2 x (4/3)π r^3.

• At high pressures, molecules interact with each other. So due to the force of attraction between the molecules, they do not strike the walls of the container. It affects the pressure exerted by molecules on the container. So the pressure exerted by the gas is lower than the ideal gas.
• Thus Pi > P or Pi =P + Pa, where Pa is a pressure correction term.

The topic ‘Van der Waals Equation’ falls under the chapter ‘States of Matter’ of class XI NCERT Chemistry. Along with the chapters ‘Chemical Bonding and Molecular Structure’, ‘Equilibrium’ and ‘Chemical Thermodynamics’, this chapter comes for a total of 21 marks.