Isosceles Triangle: Overview, Questions, Preparation

An isosceles triangle is an important topic from the chapter Triangles. A triangle has three sides and three angles, and when any two of the sides, as well as the angles opposite to these sides, are congruent or equal is known as Isosceles Triangle. If we have a triangle △XYZ and if XY = XZ similarly ∠Y = ∠Z, then this triangle will be called Isosceles Triangle. 

Source: NCERT

Types of Isosceles Triangle

There are generally 3 types of isosceles triangle:

• Isosceles Acute Triangle
• Isosceles Right Triangle
• Isosceles Obtuse Triangle

Properties of Isosceles Triangle

• The unequal side of an isosceles triangle is known as the base when 2 sides are congruent.
• The opposite angles of the two congruent sides are always equal.
• The measurement from the base to the vertex of the isosceles triangle is known as its altitude.
• The third angle of the isosceles right triangle is always 90°.

Isosceles Triangle Formulas

An isosceles triangle is a closed two-dimensional figure, and it also has a perimeter and area like other figures. The formula for

• Area (A) of isosceles triangle = ½ × h × b square units 

Here, b = base of the isosceles triangle and h = height of the isosceles triangle

• Perimeter (P) of isosceles triangle = b + 2a units, 

Here, b = base of the isosceles triangle and a = Length of the 2 congruent sides of the isosceles triangle

Apart from the isosceles triangle, there are 2 other types of triangles, and they are:
Scalene Triangle: The triangle in which no side is congruent to the other 2 sides.
Equilateral Triangle: The triangle in which all the sides and all the angles present in the triangle are congruent.

Isosceles triangle is an important topic in Class 10 mathematics exams. Every year 3 to 4 questions are asked from the respective chapter, and the weightage of the chapter ranges from 7 to 9 marks. Triangle and its applications are also covered in higher classes. The contents of the respective chapter are:

• Standards for Similarity of Triangles
• Area of Similar Triangles
• Pythagoras Theorem

1. In an △XYZ, if YZ(base) = 4cm and the height of the triangle is 6cm, then calculate the area of △XYZ. 
Solution.

We know that A = 1/2 * b * h
Therefore by applying the formula 
A = 1/2 * 4 * 6 
= 12 cm²

2. Calculate the perimeter of △XYZ, XY = ZX = 6cm and base = 4cm
Solution.

We know that P = b + 2a
Here, 
a = 6 cm
b = 4 cm, 
P = 2(6) + 4 
= 16 cm

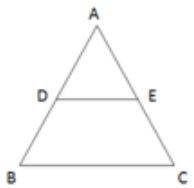
3. Show that △ABC ~ △ADE. If ∠AED = ∠ABQ.

Solution.

In △ABC and △ADE,
∠A = ∠A (Common Angle)
∠AED = ∠ABQ (Given)
Hence,
△ABC ~ △ADE.

Q: Explain the centroid of a triangle.

Q: If an equilateral triangle's each side's length is 3cm, then what will be its perimeter?

Q: What is the formula for Pythagoras Theorem?

Q: What is the total of all the interior angles of the triangle?

Q: What is Isosceles Obtuse Triangle?