Scalar Triple Product: Overview, Questions, Preparation

The triple product is a product of three three-dimensional vectors in mathematics, also known as vector algebra or Euclidean vectors. The term triple product is primarily used to represent the scalar triple product, sometimes used for vector triple product.

The scalar triple product is a resultant of the dot product of one of the vectors with the cross product of the other two vectors. For example, let us consider three vectors a,b and c. Now, their scalar triple product is represented as ( a x b ) . c

Geometric interpretation of the scalar triple product

The three vectors a,b and c define the volume of a parallelepiped in the geometric interpretation of the scalar triple product. 

We know that the volume of a parallelepiped is the product of its height with the base area. Also, the magnitude ∥a×b∥, is considered as the area of the base, and the direction of vector a x b is perpendicular to the base. Moreover, the height of the parallelepiped is also perpendicular to the direction of a x b and it is also considered as the component of c. Therefore, the height of a parallelepiped is expressed as ∥c∥ |cosϕ, where ϕ is the angle between a×b and c.

Therefore, the volume of the parallelepiped is expressed as:

Volume = ∥a × b∥ ∥c∥ |cosϕ|=|(a×b)⋅c|.

We can also represent the scalar triple product in component form using the cross product formula in component form as:

It is very necessary to find the absolute values for the volume as the scalar triple product can yield a negative or positive result or even a zero. 
Properties of the scalar triple product

Following are some of the properties of a scalar triple product:

1. The circular shift of the three vectors a, b and c ensures that there is no change in the scalar triple product.
2. The preceding property and the commutative property of the dot product ensures that there is no change in the scalar triple product with the interchange of positions by the vectors.
3. The parallelepiped will have no volume when the three vectors a, b, and c are coplanar and their scalar triple product is zero.
4. The final value of a scalar triple product is zero when there are two identical vectors.
5. The scalar triple product stands negative where there is a swapping of two vectors. This happens as a result of the anticommutativity and the circular-shift property of the cross product.

The topic scalar triple product is from the chapter vector algebra. Apart from this topic, the chapter also deals with various significant topics such as applying the scalar product of vectors, vector product of vectors, direction cosines and direction ratios of a vector, etc. The vector algebra unit accounts for a crucial 14 marks in the final examination of the 12th standard.

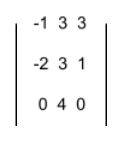
1. There three vectors a, b, and c where a = (-2,3,1), b = (0,4,0) and c = (-1,3,3). Find the volume of a parallelepiped.
Solution.

The volume of a parallelepiped is calculated using a scalar triple product.
Therefore, (a x b) . c =

= − 1(0−4) − 3(0−0) + 3(−8+0)
= 4 − 24 
= −20
Thus, the volume is I-20I = 20 cubic units.

Q: Why is the scalar triple product used?

Q: What is a scalar?

Q: Is scalar always positive?

Q: Is work a scalar quantity?

Q: What is the basic difference between a vector and a scalar?