Vipra ShrivastavaSenior Manager - Content
What is Kirchhoff’s Law?
Gustav Robert Kirchhoff was a German physicist born in Russia. His work involved researching electrical conduction. It led to him formulating two laws known as Kirchhoff's Current law and Kirchhoff's Voltage law. These laws are generally used for the analysis of circuits. They help in calculating the resistance and the flow of current in different streams through the network.
The topic 'Kirchhoff's Laws' falls under the chapter 'Current Electricity'. It is the second unit of NCERT Class 12 Physics. Along with the first unit 'Electrostatics', this unit comes for 16 marks in the exams.
What are the two Kirchhoff’s Laws?
Sometimes electrical circuits are interconnected in a complicated way. The parallel and series combination of resistors or capacitors are not always sufficient to determine all the currents and potential differences. Hence two laws known as the Kirchhoff's Laws are used for the analysis of electrical circuits. Kirchhoff's Laws are divided as:
-
Junction Rule
Also known as the Kirchhoff's Current Law(KCL), the junction rule states that at every junction the sum of the currents that enter is equivalent to the sum of the currents that leave. This rule also holds for a point in a line instead of a junction of several lines. We can understand this as when the flow of current is steady, the charges do not accumulate at any junction or point in a line. Thus, the total current(rate of flow of charge) flowing in has to be the same as the total current flowing out.
-
Loop Rule
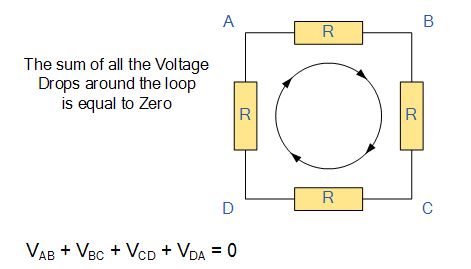
Also known as the Kirchhoff's Voltage Law (KVL), the loop rule states that the algebraic sum of the potential changes around any closed loop, with cells and resistors is zero. This rule holds because the electric potential depends on the location of a point. Starting from any point, if we return to the same point, the total change must be zero.
Kirchhoff's First Law or Junction Rule
Kirchhoff's first law is also known as Kirchhoff's junction rule. The junction rule states that the total sum of the current in a junction is equal to the total sum of currents outside it.
In simple terms, it means that the total current entering a junction is equal to the total current leaving it. There is no energy loss at the intersection.
This property of zero energy loss in Kirchoff's law is known as Conservation of charge.
Thus, I(enter) + I(exit) = 0
Kirchhoff's Second Law or Voltage Law
Kirchhoff's second law is also known as Kirchhoff's voltage law. It states that the sum of the total voltage in a closed network is always equal to 0.
This property of Kirchhoff's second law is also known as the conservation of energy.
Illustrated Examples of Kirchhoff's Law
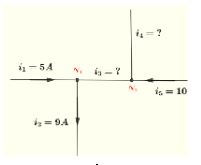
1. Find the current i3, as shown below
Solution: Currents i1 and i2 are flowing towards the node, and the currents i3 and i4 are flowing out of the node.
Apply Kirchhoff's law of current:
i1+i2 = i3+i4
Substituting,
2+9=i3+4
i3=7 A
2. Calculate the currents i3 and i4, as shown below.
Solution: i1 flows into N1, and i2 and i3 flow out of N1, hence,
i1 = i2 + i3
Substituting
5 = 9 + i3
i3=−4
Since i3 is negative, it flows into node N1
At node N2,
i3+i5 = i4
Substituting
−4+10 = i4
i4=6
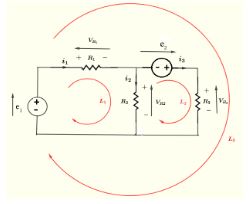
3. See the image below.
Solution: Applying Kirchhoff’s second law to loop 1,
e1−Vr1−VR2=0
Substituting,
20−5−VR2=0
VR2=15 A
Apply Kirchhoff's second law to loop 2,
Vr2+e2−VR3=0
Substituting,
15+10−VR3=0
VR3=25
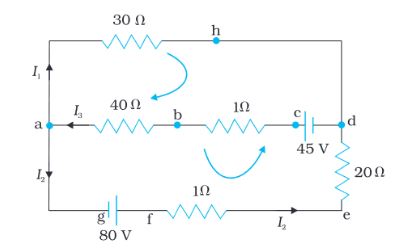
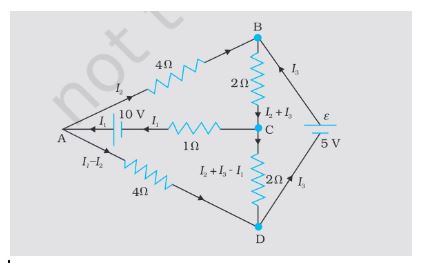
4. Given below is an electrical circuit. If I1 is 1A, find the value of I2 and I3.
FAQs on Kirchhoff’s Laws
Q: Figure 8.6 shows a capacitor made of two circular plates each of radius 12 cm, and separated by 5.0 cm. The capacitor is being charged by an external source (not shown in the figure). The charging current is constant and equal to 0.15A. (a) Calculate the capacitance and the rate of change of potential difference between the plates. (b) Obtain the displacement current across the plates. (c) Is Kirchhoff’s first rule (junction rule) valid at each plate of the capacitor? Explain.
A:
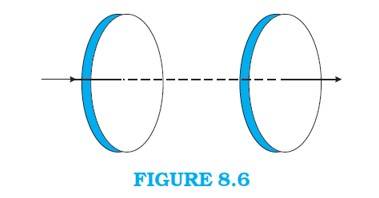
Radius of the each circular plate, r = 12 cm = 0.12
Distance between the plates, d = 5 cm = 0.05 m
Charging current, I = 0.15 A
Permittivity of free space, ε0 = 8.85 X 10−12 C2 N−1 m−2
- Capacitance between two plates is given by the relation,
C = ε0A/d , where A = Area of each plate = πr2= π X (0.12)2
C = 8.85 X 10−12 X π X (0.12)2 / 0.05 = 8.007 X 10−12 F
Charge on each plate, q = CV, where V = potential difference across plates
Differentiating both sides w.r.t. t, we get
dq/dt = C dV/dt
But dq/dt = I, therefore
dV/dt = I/C = 0.15 / 8.007 X 10−12 = 1.87 X 10−10 V/s
Therefore,the change in potential difference between the plates is 1.87 X 10−10 V/s
- The displacement current across the plates is the same as the conduction current. Hence the displacement current is 0.15 A
- Kirchhoff’s first rule is valid at each plate of the capacitor provided that we take the sum of conduction and displacement for current.
Q: What are the Kirchhoff's Laws?
A: Kirchhoff's law is applicable for the analysis of electrical circuits.
Q: What are the different Kirchhoff's Laws?
A: The Kirchhoff's laws are Kirchhoff's Current Law (Junction Rule) and Kirchhoff's Voltage Law (Loop Rule).
Q: What is the Junction Rule?
A: The junction rule is also known as Kirchhoff's Current Law (KCL) and states that at any junction the sum of the entering currents is equal to the sum of the leaving currents.
Q: What is the Loop Rule?
A: Also known as the Kirchhoff's Voltage Law (KVL), the loop rule states that the algebraic sum of the potential changes around any closed loop, involving resistors and cells in the loop, is zero.
Q: What are Kirchhoff's two rules called?
A: Kirchoff's two rules are called Kirchhoff's junction rule and Kirchhoff's loop rule.
Q: Does Kirchhoff's law fail at high frequency?
A: Yes, Kirchhoff's laws fail at high frequency.
Q: Can Kirchhoff’s laws be used for both AC and DC circuits?
A: Yes, Kirchhoff's laws can be used for both circuits.
Q: Can unknown voltages be calculated using Kirchhoff's law?
A: Yes, unknown voltages in a loop can be calculated using Kirchhoff's second law.
Q: Can unknown currents be calculated using Kirchhoff's law?
A: Yes, unknown currents can be calculated in a circuit using Kirchhoff's first law.
News & Updates
Physics Current Electricity Exam
Student Forum
Popular Courses After 12th
Exams: BHU UET | KUK Entrance Exam | JMI Entrance Exam
Bachelor of Design in Animation (BDes)
Exams: UCEED | NIFT Entrance Exam | NID Entrance Exam
BA LLB (Bachelor of Arts + Bachelor of Laws)
Exams: CLAT | AILET | LSAT India
Bachelor of Journalism & Mass Communication (BJMC)
Exams: LUACMAT | SRMHCAT | GD Goenka Test