
Salviya AntonySenior Executive - Content
Gauss's Law states that electric flux ϕE through any closed surface is equal to 1/ε0 times the net charge 'q' enclosed by the surface. This law is a fundamental principle in electromagnetism which relates the electric flux passing through a closed surface to the total charge enclosed within that surface. It has various practical applications which are important for the Class 12 physics board exam. We will discuss some applications of Gauss's Law.
Application of Gauss's Law
Following are some applications of Gauss's Law.
- Consider a charged ring of radius R on its axis at a distance x from the centre of the ring, then E = (1/4 πε0)[qx/(R2+x2)3/2
- The intensity of the electric field near a plane sheet of charge is given by E = σ/2ε0K. Here σ is the Surface charge density.
- The field between two parallel plates of a condenser is given by E = σ/ε0, while σ is the surface charge density.
Gauss's Law Applications
- Charged Spheres and Shells: Gauss's Law is useful while dealing with charged spheres and spherical shells. For instance, if we have a uniformly charged sphere, we can use a Gaussian surface (an imaginary surface) that matches the sphere's symmetry to calculate the electric field at a point outside the sphere. This simplifies the calculation considerably compared to using Coulomb's law directly.
- Flux and Charge Enclosed: Gauss's Law states that the electric flux through a closed surface is directly proportional to the net charge enclosed within that surface. We can use this relationship for determining the charge inside a closed surface even if we cannot directly observe it.
- Uniformly Charged Infinite Plane: Gauss's Law helps to simplify the calculation of the electric field due to an infinite plane with uniform charge density. By using a Gaussian surface parallel to the plane, we can show that the electric field is constant and perpendicular to the plane.
- Electric Field of a Dipole: Gauss's Law can be applied to calculate the electric field of an electric dipole. By considering a Gaussian surface that encloses both the positive and negative charges of the dipole, one can show that the electric field due to a dipole falls off as the cube of the distance, which is an important concept in understanding electric field behavior.
- Closed Surfaces and Flux: Knowing the concept of closed surfaces is important while applying Gauss's Law. The total electric flux through a closed surface (Gaussian surface) depends on the total charge enclosed within that surface. This connection is useful in understanding the relationship between electric fields and charges.
- Electric Field due to Charged Rods: We can apply Gauss's Law to determine the electric field due to a uniformly charged rod. By choosing a Gaussian cylinder around the rod, we can derive the electric field at various distances from the rod.
Gauss's Law Applications: Class 12 Physics
In conclusion, Gauss's Law and its applications is a topic of great importance for the Class 12 students who are preparing for various board exams JEE, NEET, and other entrance exams.
FAQs on Applications of Gauss's Law
Q: An infinite line charge produces a field of 9 ×10^4 N/C at a distance of 2 cm. Calculate the linear charge density.
A: Electric field produced by the infinite line charge at a distance d having linear charge density λ is given by
E = λ / 2π ∈0 d2, where
E = Electric field = 9 X 104 N/C
where ∈0 = Permittivity of free space = 8.854 X 10-12 C2N-1m-2
d = 2 cm = 0.02 m
Hence, = 9 X 104 X 2X π X 8.854 X 10-12X 0.02 = 10μC/m
Q: Two large, thin metal plates are parallel and close to each other. On their inner faces, the plates have surface charge densities of opposite signs and of magnitude 17.0 ×10^(-22) C/m^2. What is E: (a) in the outer region of the first plate, (b) in the outer region of the second plate, and (c) between the plates?
A: The given conditions are explained in the adjacent diagram
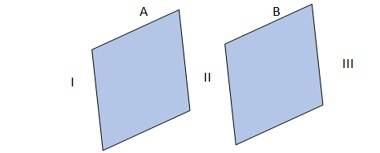
Where A and B represent two large, thin metal plates, parallel and close to each other. The outer surface of A is shown as I, outer surface of B is shown as II and the surface in between A and B is shown as III.
Charge density of plate A, σ = 17.0 X 10-22 C/m2
Charge density of plate B, σ = 17.0 X 10-22 C/m2
- & (b) In the region, I and III, electric field E is zero, because charge is not enclosed by the respective plates.
(c) Electric field, E in the region II is given by
E = σ / ∈0
where ∈0 = Permittivity of free space = 8.854 X 10-12 C2N-1m-2
E = 17.0 X 10-22 / 8.854 X 10-12N/C = 1.92 X 10-10 N/C
Q: An oil drop of 12 excess electrons is held stationary under a constant electric field of 2.55 ×10^4 NC^(-1)(Millikan’s oil drop experiment). The density of the oil is 1.26 g / cm^3. Estimate the radius of the drop. (g = 9.81 m/s^2; e = 1.60 ×10^(-19) C).
A:Excess electrons on an oil drop, n = 12
Electric field intensity, E = 2.55 X 104 NC-1
Density of oil, ρ = 1.26 g / cm3 = 1.26 X 103 g/m3
Acceleration due to gravity, g = 9.81 m/s2
Charge of an electron, e = 1.60 X 10-19 C
Let the radius of the oil drop be r
Force (F) due to electric field (E) is equal to the weight of the oil drop (W)
F = W
Eq = mg
Ene = 4/3πr3 X ρ X g
r3 = 3 X E x n X e / 4 X π X ρ X g = 3 X 2.55 X 104X12 X1.60 X 10-19 / 4 xπ x 1.26 X 103 X 9.81 = r = 9.815 X 10-7 m = 9.815 X 10-4 mm
News & Updates
Physics Current Electricity Exam
Student Forum
Popular Courses After 12th
Exams: BHU UET | KUK Entrance Exam | JMI Entrance Exam
Bachelor of Design in Animation (BDes)
Exams: UCEED | NIFT Entrance Exam | NID Entrance Exam
BA LLB (Bachelor of Arts + Bachelor of Laws)
Exams: CLAT | AILET | LSAT India
Bachelor of Journalism & Mass Communication (BJMC)
Exams: LUACMAT | SRMHCAT | GD Goenka Test