The universe is a vast expanse of interconnected forces and phenomena, and at the heart of this intricate web lies electromagnetism—a force that powers our modern world. To comprehend the profound principles governing electric fields, charges, and their interactions, one must delve into Gauss's Law. In this article, we will delve into the depths of Gauss's Law as presented in Class XII NCERT curriculum, unraveling its significance and real-world applications.
Introduction to Gauss's Law:
Gauss's Law is a fundamental concept in electromagnetism that elucidates the relationship between electric charges and the electric field they create. It was formulated by the brilliant mathematician and physicist Carl Friedrich Gauss and remains a cornerstone of modern physics. The law provides a powerful tool to simplify complex electric field problems by relating the electric flux passing through a closed surface to the enclosed charge.
Mathematical Formulation:
Gauss's Law is succinctly expressed in mathematical terms:
ϕ = q/ε0
Where,
ϕ = The flow of electricity across a closed surface S containing any volume V
Q = entire charge contained within V
ε0 = The electric constant
Φ = → E.d → A = qnet/ε0
Key Insights and Applications:
Understanding Gauss's Law opens the door to a plethora of insights and practical applications:
Symmetry and Simplification: Gauss's Law proves invaluable when dealing with symmetrical charge distributions. It simplifies complex problems by exploiting the inherent symmetry to determine electric fields without intricate calculations.
Charged Conductors: The law aids in comprehending how charges distribute themselves on conductive surfaces. For instance, the electric field within a conductor in electrostatic equilibrium is zero, a result derived from Gauss's Law.
Insight into Nature: Gauss's Law provides insights into the nature of electric fields emanating from different charge configurations, whether they are point charges, charged spheres, or other geometries.
Electrostatic Shielding: Understanding Gauss's Law helps engineers design effective shielding mechanisms against unwanted electric fields, ensuring safety in various technological applications.
Visualizing Gauss's Law:
Gauss's Law is not just confined to mathematical equations; it offers a profound visual understanding of electric fields and charges. The law emphasizes that electric field lines emerge from positive charges and terminate on negative charges, effectively visualizing the electric interactions.
Conclusion:
As Class XII NCERT students, delving into Gauss's Law unlocks the door to a deeper understanding of electromagnetism, charges, and electric fields. The law's mathematical elegance and practical utility make it an essential tool for scientists, engineers, and researchers. Through its exploration, you embark on a journey that connects the theoretical foundation of electromagnetism with its real-world applications. By mastering Gauss's Law, you are poised to unravel the mysteries of electric phenomena and contribute to the ongoing scientific advancements that shape our world.
FAQs on Gauss Law
Q: A system has two charges q_A= 2.5×10^(-7) C and q_B= –2.5×10^(-7)C located at points A: (0, 0, –15 cm) and B: (0,0, +15 cm), respectively. What are the total charge and electric dipole moment of the system?
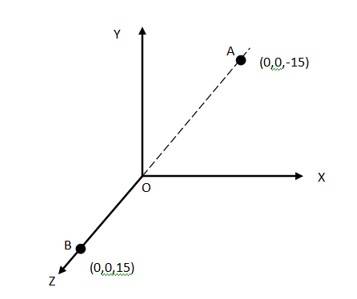
At A, the amount of charge, qA = 2.5 × 10-7 C
At B, the amount of charge, qB = -2.5 × 10-7 C
Total charge of the system, q = qA + qB = 0
Distance between two charges at point A and B = 15 + 15 = 30 cm = 0.3 m
Electric dipole moment of the system is given by p = qA X d = qB X d = 2.5 × 10-7 X 0.3 = 7.5 × 10-8 C m, along positive z axis.
Q: An electric dipole with dipole moment 4 ×10^(-9) C m is aligned at 30° with the direction of a uniform electric field of magnitude 5 ×10^4 NC^(-1). Calculate the magnitude of the torque acting on the dipole.
A: Electric dipole moment, p = 4 × 10-9 C m
Angle made by p with a uniform electric field, θ = 30°
Electric field, E = 5 × 104 NC-1
Torque acting on the dipole is given by ζ= pESinθ = 4 × 10-9 X 5 × 104 X sin 30°
= 1 × 10-4 Nm
Therefore, the magnitude of the torque acting on the dipole is 10-4 Nm
Q: A polythene piece rubbed with wool is found to have a negative charge of 3 ×10^(-7)C. (a) Estimate the number of electrons transferred (from which to which?) (b) Is there a transfer of mass from wool to polythene?
A: When polythene rubbed against wool, a number of electrons get transferred from wool to polythene. Hence, wool becomes positively charged and polythene negatively charged.
Amount of charge on the polythene piece, q = -3 X 10-7 C.
Amount of charge of 1 electron e = -1.6 X 1019
So number of electron transferred from wool to polythene= -2 X 10-7 X-1.6 X 1019= 1.875X 1012
- (b)Since electron has a mass, so there will be transfer of mass also.
Mass of single electron me = 9.1 X 10-31 kg
Total mass transferred from wool to polythene = 1.875 X 1012 X 9.1 X 10-31 kg
= 1.706 X 10-18 kg negligible
Hence a negligible amount of mass is transferred from wool to polythene.
Q: (a) Two insulated charged copper spheres A and B have their centers separated by a distance of 50 cm. What is the mutual force of electrostatic repulsion if the charge on each is 6.5 ×10^(-7) C? The radii of A and B are negligible compared to the distance of separation. (b) What is the force of repulsion if each sphere is charged double the above amount, and the distance between them is halved?
- A: Charge on sphere A, qA = 6.5 X 10-7 C
Charge on sphere B, qB = 6.5 X 10-7 C
Distance between the spheres, r = 50 cm = 0.5 m
Force of repulsion between two spheres
F = 1/4π∈0 X q1q2 / r2, where ∈0 = Permittivity of free space = 8.854 X 10-12 C2N-1m-2
Hence, F = 1 / 4Xπ x 8.854 X 10-12 X 6.5 × 10-7 X 6.5 × 10-7 / (0.5)2 = N = 0.0152 N = 1.52 X 10-2 N
- Charge on sphere A, qA = 2 X 6.5 X 10-7 C = 1.3 X 10-6 C
Charge on sphere B, qB = 2 X 6.5 X 10-7 C = 1.3 X 10-6 C
Distance between the spheres, r = 50/2 = 25 cm = 0.25 m
Force of repulsion between two spheres
F = 1/4π∈0 X q1q2 / r2, where ∈0 = Permittivity of free space = 8.854 X 10-12 C2N-1m-2
Hence, F = 1 / 4Xπ x 8.854 X 10-12 X 1.3 × 10-6 X 1.3 × 10-6 / (0.25)2 = N = 0.243 N
Q: Suppose the spheres A and B in Exercise 1.12 have identical sizes. A third sphere of the same size but uncharged is brought in contact with the first, then brought in contact with the second, and finally removed from both. What is the new force of repulsion between A and B?
A: When the third uncharged sphere C is brought in contact with the sphere A, then the charge is shared and becomes half. Then
- qA = q/2 and qc = q/2
When the charged sphere C is brought in contact with charged sphere B, the charge between both the sphere is shared and becomes half
- qB, qC = 1/2(q + q/2) = (3q/4)
Hence the force of repulsion between sphere A and B can be given as
F = 1/4π∈0 X q1q2 / r2, where ∈0 = Permittivity of free space = 8.854 X 10-12 C2N-1m-2
Hence, F = 1 / 4Xπ x 8.854 X 10-12 X (q/2 X 3q/4 X (0.5)2 ) X 1 / 4Xπ x 8.854 X 10-12 X (3 X q2/ 8X (0.5)2 = N = 0.243 N
= 1 / 4Xπ x 8.854 X 10-12 X (3 X ( 6.5 X 10-7)2/ 8X (0.5)2
= 5.695 X 10-3 N
Q: Figure 1.33 shows tracks of three charged particles in a uniform electrostatic field. Give the signs of the three charges. Which particle has the highest charge to mass ratio?
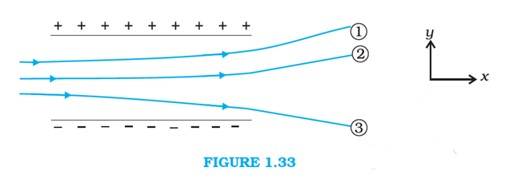
Since the charges 1 & 2 are attracted towards + ve, their charges will be – ve. The charge 3 is attracted towards – ve, hence its charge will be +ve.
The charge to mass ratio (emf) is directly proportional to the displacement, charge 3 will have the highest charge to mass ratio.
Q: Consider a uniform electric field E = 3 ×10^3 î N/C. (a) What is the flux of this field through a square of 10 cm on a side whose plane is parallel to the yz plane? (b) What is the flux through the same square if the normal to its plane makes a 60° angle with the x-axis?
A: Electric field intensity, E = 3 X 103 î N/C
Magnitude of electric field intensity, |E| = |3 X 103| N/C
Side of the square, s = 10 cm = 0.1 m
Area of the square, A = s2 = 0.01m2
The plane of the square is parallel to the y-z plane, hence the angle between the unit vector normal to the plane and electric field, θ = 0°
Flux (ψ) through the plane is given by the relation, ψ = |E| A cos θ = 3 X 103 X 0.01X cos 0° = 30 Nm2/ C
- When the normal to its plane make a 60° angle with x-axis, θ = 60° . From the equation ψ = |E| A cos θ, we get ψ = 3 X 103 X 0.01X cos 60°= we get = 15 Nm2/ C
Q: What is the net flux of the uniform electric field of Exercise 1.15 through a cube of side 20 cm oriented so that its faces are parallel to the coordinate planes?
A: When the cube side is oriented so that its faces are parallel to the coordinate planes, number of field lines entering the cube is equal to the number of field lines piercing out of the cube. A as a result, net flux through the cube is zero.
Q: Careful measurement of the electric field at the surface of a black box indicates that the net outward flux through the surface of the box is 8.0 × 10^3 Nm^2/C. (a) What is the net charge inside the box? (b) If the net outward flux through the surface of the box were zero, could you conclude that there were no charges inside the box? Why or Why not?
A: Net outward flux through the surface of the box ψ, = 8.0 × 103 Nm2 /C
For a body containing net charge q, flux is given by the relation, ψ = q/ ∈0
where ∈0 = Permittivity of free space = 8.854 X 10-12 C2N-1m-2
Hence q = ψ X ∈0 = 8.0 × 103 X 8.854 X 10-12 C = 7.0832 X 10-8 C
= 7.0832 X 10-2 µC
- Net flux piercing out through a body depends on the net charge contained in the body. If net flux is zero, then it can be inferred that the net charge inside the body is zero. The body may have equal amount of positive and negative charges.
Q: A point charge +10 μC is a distance 5 cm directly above the centre of a square of side 10 cm, as shown in Fig. 1.34. What is the magnitude of the electric flux through the square? (Hint: Think of the square as one face of a cube with edge 10 cm.)

Q: A point charge of 2.0 μC is at the centre of a cubic Gaussian surface 9.0 cm on edge. What is the net electric flux through the surface?
A:
Q: A point charge causes an electric flux of –1.0 ×10^3 Nm^2/C to pass through a spherical Gaussian surface of 10.0 cm radius centered on the charge. (a) If the radius of the Gaussian surface were doubled, how much flux would pass through the surface? (b) What is the value of the point charge?
A: Electric flux, ψ = –1.0 X 103 Nm2 /C
Radius of Gaussian surface, r = 10 cm = 0.1 m
- Electric flux piercing through a surface depends on the net charge enclosed inside a body, not on the size of the body. Hence, if the radius is doubled, the net flux passing does not change. The net flux passing will remain as -1 X 103 Nm2 /C
- The relation between point charge and the electric flux is given by, ψ = q/∈0
where ∈0 = Permittivity of free space = 8.854 X 10-12 C2N-1m-2
Hence point charge q = ψ X ∈0 = –1.0 X 103 X 8.854 X 10-12 C = - 8.854 X 10-9 C
= - 8.854 X 10-3 µC
Q: A conducting sphere of radius 10 cm has an unknown charge. If the electric field 20 cm from the centre of the sphere is 1.5 ×10^(3 )N/C and points radially inward, what is the net charge on the sphere?
A: Electric field intensity, E, at a distance d, from the centre of a sphere containing net charge q is given by the relation,
E = 1/4π ∈0 X q/d2
where ∈0 = Permittivity of free space = 8.854 X 10-12 C2N-1m-2
q = Net charge
E = 1.5 X 103 N/C
d = 2r = 20 cm = 0.2 m
q = E X4π ∈0 X d2 = 1.5 X 103 X 4 X π X 8.854 X 10-12X (0.2)2 C = 6.67 X 10-9 C
= 6.67 nC
The net charge on the sphere is 6.67 nC
Q: A uniformly charged conducting sphere of 2.4 m diameter has a surface charge density of 80.0 μC/m^2. (a) Find the charge on the sphere. (b) What is the total electric flux leaving the surface of the sphere?
A: Diameter of the sphere, d = 2.4 m, Radius, r = 1.2 m
Surface charge density, σ = 80 μC/m2 = 80 X 10-6 C/m2
Total charge on the surface of the sphere is given by Q = σA, where A = surface area of the sphere = 4πr2
Hence Q = 80 X 10-6 X 4 X π X (1.2)2 C = 1.447 X 10-3 C
Q: An infinite line charge produces a field of 9 ×10^4 N/C at a distance of 2 cm. Calculate the linear charge density.
A: Electric field produced by the infinite line charge at a distance d having linear charge density λ is given by
E = λ / 2π ∈0 d2, where
E = Electric field = 9 X 104 N/C
where ∈0 = Permittivity of free space = 8.854 X 10-12 C2N-1m-2
d = 2 cm = 0.02 m
Hence, = 9 X 104 X 2X π X 8.854 X 10-12X 0.02 = 10μC/m
Q: Two large, thin metal plates are parallel and close to each other. On their inner faces, the plates have surface charge densities of opposite signs and of magnitude 17.0 ×10^(-22) C/m^2. What is E: (a) in the outer region of the first plate, (b) in the outer region of the second plate, and (c) between the plates?
A: The given conditions are explained in the adjacent diagram
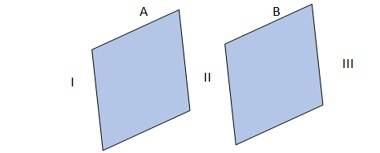
Where A and B represent two large, thin metal plates, parallel and close to each other. The outer surface of A is shown as I, outer surface of B is shown as II and the surface in between A and B is shown as III.
Charge density of plate A, σ = 17.0 X 10-22 C/m2
Charge density of plate B, σ = 17.0 X 10-22 C/m2
- & (b) In the region, I and III, electric field E is zero, because charge is not enclosed by the respective plates.
(c) Electric field, E in the region II is given by
E = σ / ∈0
where ∈0 = Permittivity of free space = 8.854 X 10-12 C2N-1m-2
E = 17.0 X 10-22 / 8.854 X 10-12N/C = 1.92 X 10-10 N/C
Q: An oil drop of 12 excess electrons is held stationary under a constant electric field of 2.55 ×10^4 NC^(-1)(Millikan’s oil drop experiment). The density of the oil is 1.26 g / cm^3. Estimate the radius of the drop. (g = 9.81 m/s^2; e = 1.60 ×10^(-19) C).
A: Excess electrons on an oil drop, n = 12
Electric field intensity, E = 2.55 X 104 NC-1
Density of oil, ρ = 1.26 g / cm3 = 1.26 X 103 g/m3
Acceleration due to gravity, g = 9.81 m/s2
Charge of an electron, e = 1.60 X 10-19 C
Let the radius of the oil drop be r
Force (F) due to electric field (E) is equal to the weight of the oil drop (W)
F = W
Eq = mg
Ene = 4/3πr3 X ρ X g
r3 = 3 X E x n X e / 4 X π X ρ X g = 3 X 2.55 X 104X12 X1.60 X 10-19 / 4 xπ x 1.26 X 103 X 9.81 = r = 9.815 X 10-7 m = 9.815 X 10-4 mm
News & Updates
Physics Current Electricity Exam
Student Forum
Popular Courses After 12th
Exams: BHU UET | KUK Entrance Exam | JMI Entrance Exam
Bachelor of Design in Animation (BDes)
Exams: UCEED | NIFT Entrance Exam | NID Entrance Exam
BA LLB (Bachelor of Arts + Bachelor of Laws)
Exams: CLAT | AILET | LSAT India
Bachelor of Journalism & Mass Communication (BJMC)
Exams: LUACMAT | SRMHCAT | GD Goenka Test
