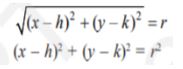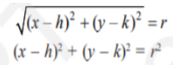Rachit Kumar SaxenaManager-Editorial
What is Circle?
The circle is one of the most important topics in two-dimensional geometry. A circle is the locus of a point that maintains a constant distance from a fixed point. This fixed point is called the centre. The distance from the circle’s centre to any point on the circle is called the circle’s radius.
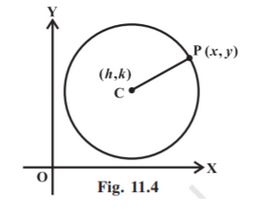
The simplest form of the equation of a circle is when the circle’s centre lies at the origin (0, 0). Let the centre of the circle be at a fixed point C (h, k) and the length of the radius be equal to r. If P(x, y) be the moving point on the circle, we have the definition | CP| = r. Therefore the equation is:
This is the standard form of the equation of the circle.
Some Particular Cases
If the centre is at the origin and the radius r, then h = 0, k=0, and the equation of the circle is x2+y2 = r2. Note - this is called the standard form of the equation of a circle.
If the origin lies on the circle then h2+k2 = r2, and so the equation of the circle in this case is x2+y2 -2hx -2ky = 0.
If the centre lies at the x-axis, then the centre’s ordinate is zero, i.e. k=0, and so the equation of the circle is (x-h)2 + y2 = r2.
General Equation of a Circle
The general equation of the circle is given by x2+y2 + 2gx + 2fy + c =0, where, g, f and c are constants.
The centre of this circle is ( - g, -f )
The radius of the circle is √(g2+ f2 -c)
The general equation of a circle passing through the origin is given by x2+y2 -2gx -2fy = 0.
Weightage of Circle
The topic is from Conic Sections in Class 11th maths. It carries 5-8 marks.
In this chapter, students learn different curves like circle, parabola, hyperbola, and ellipse. These intersections are obtained from different sections of two cones conjoined at the tip.
Illustrated Examples on Circle
1: Equation of the circle whose centre is at ( -5, 4) and the radius is 7 is –
Solution. (x+5)2 + (y-4)2 = 72
i.e., x2+ y2+ 10x - 8y- 8 = 0.
2. Find the centre and the radius of the circle x2 + y2+ 8x + 10y – 8 = 0.
Solution. The given equation is (x2 + 8x) + (y2 + 10y) = 8
Now, completing the squares within the parenthesis,
we get (x2+ 8x + 16) + (y2 + 10y + 25) = 8 + 16 + 25 i.e. (x + 4)2 + (y + 5)2 = 49 i.e. {x – (– 4)}2 + {y – (–5)}2 = 72.
Therefore, the given circle has a centre at (– 4, –5) and radius 7.
Image Source: NCERT
FAQs on Circle
Q: What is the standard form?
Q: What is an easy trick to remember the form?
Q: What should we keep in mind when a circle passes through the origin?
Q: What are the different forms of equations of a circle?
Q: How did ‘conic sections’ come into existence?
News & Updates
Maths Conic Sections Exam
Student Forum
Popular Courses After 12th
Exams: BHU UET | KUK Entrance Exam | JMI Entrance Exam
Bachelor of Design in Animation (BDes)
Exams: UCEED | NIFT Entrance Exam | NID Entrance Exam
BA LLB (Bachelor of Arts + Bachelor of Laws)
Exams: CLAT | AILET | LSAT India
Bachelor of Journalism & Mass Communication (BJMC)
Exams: LUACMAT | SRMHCAT | GD Goenka Test