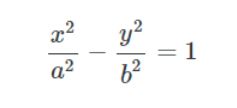Hyperbola: Overview, Questions, Preparation

In Mathematics, Hyperbola is a division of conic sections. If a cone's surface intersects with a plane, then curves are formed. It is an open curve with two outward arms which is called Hyperbola.

A hyperbola collects all the points in a plane with a persistent distance between two fixed points and each point.

Conjugate Axis and Traverse Axis: 

Traverse Axis: It is a line segment that passes through the hyperbola’s centre. It has vertices as the endpoints. The foci of the hyperbola lie on the transverse axis.

Conjugate Axis: This axis is perpendicular to the transverse axis. Its endpoints are two co-vertices. 

Eccentricity of Hyperbola

The distance ratio from vertex to centre and from foci to the centre is called hyperbola's eccentricity. 

Let e denote Eccentricity. 

So,  e = c/a

Since c ≥ a hence, the eccentricity is greater than 1 in the case of hyperbola always. 

Standard Equation of Hyperbola

The simple way to determine the hyperbola's standard equation is to assume that a hyperbola's centre is the origin (0,0). Its foci line is either on the y-axis or x-axis of the Cartesian Plane.

The segment line perpendicular to the transverse axis via any foci so that their endpoints lie on the hyperbola is known as the latus rectum of a hyperbola.

Hyperbola topic is significant in class 12th standard as hyperbola carries most of the weightage in Conic Sections chapter. In class 12th final year examinations, 3 to 4 questions are asked from the Hyperbola chapter in Mathematics for around 10-12 marks. 

1. Find the circle equation that passes through (2, – 2), and (3,4). Its centre lies on the line whose equation is x + y = 2.

Solution. Let the circle’s equation be (x – h)² + (y – k)² = r² .

As given, the circle passes through (2, – 2) and (3,4). 

We, now, have (2 – h) ² + (–2 – k) ² = r² .....(1)

Also,  (3 – h)² + (4 – k)² = r² ..... (2)

It is also given that the centre of the circle lies on the given line equation x + y = 2,

We, now, have h + k = 2 ..... (3)

Solving eq (1), (2) and (3)

We have h = 0.7, k = 1.3 and r2 = 12.58 as results. 

Therefore,  the required circle’s equation is (x – 0.7)² + (y – 1.3)² = 12.58.

2. Find the circle’s question whose centre is at (0,0) and radius r.

Solution. Here h = k = 0. T
Therefore, the given circle’s equation is x² + y² = r²

3. Find the circle’s equation with the given values. 

Centre (–3, 2)

Radius= 4

Solution. Here h = –3, k = 2 and r = 4.

Therefore, the required circle’s equation is (x + 3)² + (y –2)² = 16.

Q: What is the standard hyperbola equation?

Q: How do you define hyperbola in Physics?

Q: Can we say hyperbola as a function?

Q: Does hyperbola have a continuous curve?

Q: How is a hyperbola made?