- What is Eccentricity?
- Weightage of Eccentricity
- Illustrative Examples on Eccentricity
- FAQs on Eccentricity
What is Eccentricity?
Eccentricity is a concept in the conic section. It can be defined as how much deviation has occurred for any shape from the uniform circularity around a point, given the nature of the shape. There are a few different types of conic sections in geometry. These may be a parabola, hyperbola, ellipse, and circle.
Eccentricity of Conic Sections
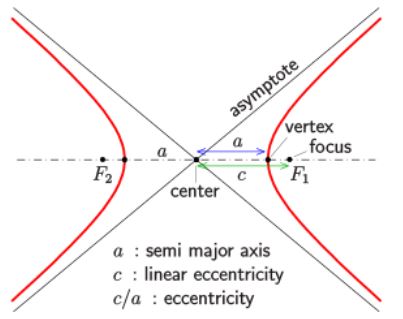
The eccentricity can be defined as the distance between any point to its fixed-point or focus- divided by the perpendicular distance from the focus to its closest directrix. This value is constant for any conic section.
Eccentricity, which is denoted by ‘e’ = c/a
Where,
c = distance from the focus to the centre
a = distance from the vertex to the centre
The following are a few of the essential shapes and their eccentricity equations:
Eccentricity of Parabola:
The general equation to find out the eccentricity of a parabola is given by the equation x2 = 4ay. And, the eccentricity of a parabola is equal to 1.
Eccentricity of Ellipse:
The general equation of an ellipse is given by the formula x2/a2 +y2/b2 =1. And, the eccentricity of an ellipse is less than 1. Thus, the eccentricity formula of an ellipse is given by the general equation √(1-b2/a2).
In the above equations, ‘a’ and ‘b’ are called the semi-major axis and semi-minor axis lengths, respectively.
Eccentricity of Hyperbola:
The general equation of a hyperbola is given by the formula x2/a2 - y2/b2 = 1. And, the eccentricity of a hyperbola is greater than 1. Thus, the eccentricity formula for a hyperbola is given by the general equation √(1+ b2/a2).
In the above equations, ‘a’ and ‘b’ are called the semi-major and semi-minor axes’ lengths respectively.
Weightage of Eccentricity
This topic is taught in classes 11 and 12 according to the prescribed NCERT norms. It is also important for competitive exams. A student can expect 1 2-3 mark questions and one 6 mark questions from this topic.
Illustrative Examples on Eccentricity
1. Find the eccentricity of the ellipse for the given equation 16x2 + 25y2 = 400
Solution: It is given that:
16x2 + 25y2 = 400
The general equation for any ellipse:
x2/a2+y2/b2= 1
So to convert the given information to its general form we get: 16x2/400 + 25y2/400 =1
Solving this we get a=5 and b=4.
To find the eccentricity, we need to substitute the values of a, b, and simplify the form.
The general form:
√(1-b2/a2).
After solving the above form, we will get that the e=⅗ for this ellipse.
FAQs on Eccentricity
Q: What is eccentricity in mathematics?
Q: How to find the eccentricity of a parabola?
Q: What are the different types of conics?
Q: What is an ellipse?
Q: What is the eccentricity of a circle?
A: The equation of the circle with centre ‘C(h, k)’ with a radius ‘r’ is (x –h)2+(y–k)2= r2 where the point of origin of the circle is at the origin on a cartesian plane. And, the eccentricity of a circle is equal to 0.
Maths Conic Sections Exam
Student Forum
Popular Courses After 12th
Exams accepted
CA FoundationExams accepted
ICSI ExamExams accepted
BHU UET | GLAET | GD Goenka TestBachelor of Business Administration & Bachelor of Law
Exams accepted
CLAT | LSAT India | AIBEExams accepted
IPMAT | NMIMS - NPAT | SET
Exams accepted
BHU UET | KUK Entrance Exam | JMI Entrance ExamBachelor of Design in Animation (BDes)
Exams accepted
UCEED | NIFT Entrance Exam | NID Entrance ExamBA LLB (Bachelor of Arts + Bachelor of Laws)
Exams accepted
CLAT | AILET | LSAT IndiaBachelor of Journalism & Mass Communication (BJMC)
Exams accepted
LUACMAT | SRMHCAT | GD Goenka Test