- What are the Applications of Integrals?
- Illustrated Examples on Application of Integrals
- FAQs on Application on Integrals
What are the Applications of Integrals?
Integration is the reverse function of a differential and is represented by ∫. It has numerous applications in the fields of mathematics and science and some of these applications are:-
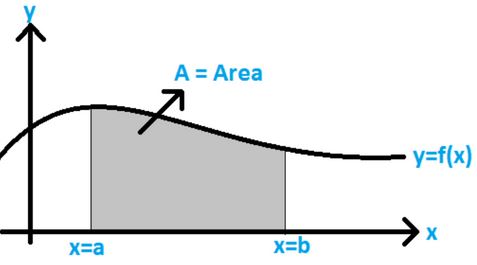
Area under a curve
To understand how we can find the area under a simple curve, consider a curve function:
y = f(x)
On a graph, draw the curve and two straight lines x=a and x=b ( where b>a ). Imagine the area bounded by the curve between the two straight lines as a collection of several thin strips.
Consider a strip and assign its height as y and its breadth as dx. This arbitrary strip is called the Elementary Area.
Area of the strip: dA = y dx
y = f(x) and dx is a small value between a and b
Now, the area under the curve is the total area of all the individual strips.
Total area:, A =a∫b dA = a∫b y dx = a∫b f(x) dx
The area between a curve and a line
The same formula can be applied to find the area bounded by a circle, parabola, or an ellipse and a line. Represent the lines and the curves on the x-y axis before solving the problem.
The area between two curves
Consider two curves represented by y = f(x) and y = g(x)
These curves will intersect at point x=a and x=b
Area between curves = ∫ab [f(x) -g(x)] dx
Where f(x) > g(x) in [a,b]
Details about the topic
Integration and its applications are introduced to higher class levels and is taught to students in grade 12 as a part of Calculus. The concepts of integrals are used in different scientific modules and complex mathematical functions.
Illustrated Examples on Application of Integrals
Find the area of the region bounded by the curve y2 = x and the lines x = 1, x = 4, and the x-axis in the first quadrant.
y2 = x
y = √x
Area under the curve = 1∫4 y dx = 1∫4 √x dx
= [x3/2 ÷ 3/2 ]14
= ⅔ [43/2 - 13/2 ] = 14/3 unit2
2. The area between x = y2 and x = 4 is divided into two equal parts by the line x = a. Find the value of a.
Solution.
y2 = x
y = √x
Area 1 = area between origin and line x=a
Area 2 = area between line x=a and x=4
Area 1 = Area 2
0∫a √x dx = a∫4 √x dx
⅔ a3/2 = ⅔ [ 8 - a3/2 ]
a3/2 =4
a = 42/3
3. Using integration find the area of the triangular region whose sides have the
equations y = 2x + 1, y = 3x + 1 and x = 4.
Solution. Use the equations to find the vertices of the triangle
A (0,1)
B (4,13)
C (4,9)
The area of the triangle is obtained by subtracting the area under the line y = 2x + 1 from the area under the line y = 3x + 1
= 0∫1 (3x + 1)dx - 0∫1 (2x + 1)dx
= [3x2/2 + x - (2x2/2 +x) ]14
= 8 unit2
FAQs on Application on Integrals
Q: What can integration be used for?
Q: How can you calculate the area bounded by a curve on the y axis?
Area = ∫cd f(y) dy
where y=c and y=d are the two horizontal lines and c
Q: What function represents a circle?
Q: What is the area enclosed by the ellipse x/a2 + y/b2 =1 ?
Q: What is the area enclosed by the circle x2 +y2= a2?
Maths Integrals Exam
Student Forum
Popular Courses After 12th
Exams accepted
CA FoundationExams accepted
ICSI ExamExams accepted
BHU UET | GLAET | GD Goenka TestBachelor of Business Administration & Bachelor of Law
Exams accepted
CLAT | LSAT India | AIBEExams accepted
IPMAT | NMIMS - NPAT | SET
Exams accepted
BHU UET | KUK Entrance Exam | JMI Entrance ExamBachelor of Design in Animation (BDes)
Exams accepted
UCEED | NIFT Entrance Exam | NID Entrance ExamBA LLB (Bachelor of Arts + Bachelor of Laws)
Exams accepted
CLAT | AILET | LSAT IndiaBachelor of Journalism & Mass Communication (BJMC)
Exams accepted
LUACMAT | SRMHCAT | GD Goenka Test