Rachit Kumar SaxenaManager-Editorial
What are Venn Diagrams?
Venn diagrams are essential pictorial representations of sets using circles. They are used to represent individual sets and depict operations between sets and showcase relations between two or more sets. They were first introduced by John Venn in the 19th Century, and are also called set diagrams or logic diagrams. Set operations such as union and intersection, as well as arithmetic operations such as addition and subtraction.
Sets are fundamental to the wide world of statistics. Though seemingly simple, the Set Theory is used widely for statistical analysis and representation of large groups of data. It is imperative that students gain a firm grasp over the set theory, and the various topics included in it, at a very early stage. For many students, the set theory is synonymous with Venn diagrams.
Venn diagrams are a significant part of the set theory, and this is very evident from the way in which they are explained in the NCERT Mathematics Textbook of Class XI. The process of drawing Venn diagrams is explained from scratch, using one, two, and three sets. Further in the chapter, Venn diagrams are used wherever possible to explain set theorems and operations. From the exam point of view, Venn diagrams are essential in almost every set theory-related question you will attempt. The individual weightage of drawing Venn diagrams in these questions might be less, but they can be an essential step in both 4 marks and 6 mark questions. Application-based questions concerning the Set Theory almost necessarily involve the usage of Venn diagrams for the explanation.
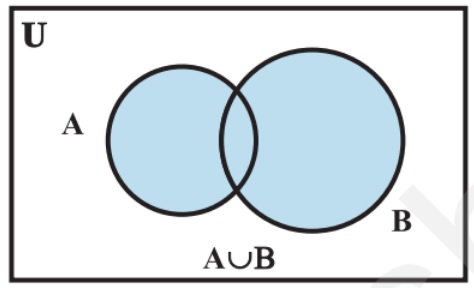
Set Operations Using Venn Diagrams
Image Source: NCERT
Venn diagrams can also be used to show subsets and complements of sets. In a Venn diagram, it isn’t just the circles that depict the sets that are important. The box that encloses these circles is also a part of the Venn diagram and is equally important. This is because the region interior to this box represents the universal set.
Using the Venn diagram, you cannot just depict the complements of individual sets, but also the complements of unions and intersections of two or more sets. These are difficult to express using set equations, but Venn diagrams make them easier.
Importance and Weightage
Venn diagrams are a significant part of the set theory, and this is very evident from the way in which they are explained in the NCERT Mathematics Textbook of Class XI. The process of drawing Venn diagrams is explained from scratch, using one, two, and three sets. Further in the chapter, Venn diagrams are used wherever possible to explain set theorems and operations. From the exam point of view, Venn diagrams are essential in almost every set theory-related question you will attempt. The individual weightage of drawing Venn diagrams in these questions might be less, but they can be an essential step in both 4 marks and 6 mark questions. Application-based questions concerning the Set Theory almost necessarily involve the usage of Venn diagrams for the explanation.
Illustrated Examples of Venn Diagram
1. Set A is the set of all non-negative real numbers. Set B is the set of whole numbers. What is the intersection of A and B?
Solution. The intersection of A and B is the number 0.
If Set A has 10 elements, Set B has 4 elements, and both sets have 2 elements in common, how many elements does the union of A and B have?
The union of A and B has n(A) + n(B) - n(AB) elements
= 10 + 4 - 2
= 12
2. What is the complement of the set of rational numbers, if the universal set is the set of real numbers?
Solution. The complement of the set of rational numbers is the set of irrational numbers.
FAQs for Venn Diagram
Q: What set operations can be expressed using a Venn diagram?
Q: What is the box in a Venn diagram?
Q: How can you depict the complement of a set using a Venn diagram?
Q: How can you depict disjoint sets in a Venn diagram?
Q: How do you express the intersection of two sets in a Venn diagram?
News & Updates
Maths Sets Exam
Student Forum
Popular Courses After 12th
Exams: BHU UET | KUK Entrance Exam | JMI Entrance Exam
Bachelor of Design in Animation (BDes)
Exams: UCEED | NIFT Entrance Exam | NID Entrance Exam
BA LLB (Bachelor of Arts + Bachelor of Laws)
Exams: CLAT | AILET | LSAT India
Bachelor of Journalism & Mass Communication (BJMC)
Exams: LUACMAT | SRMHCAT | GD Goenka Test