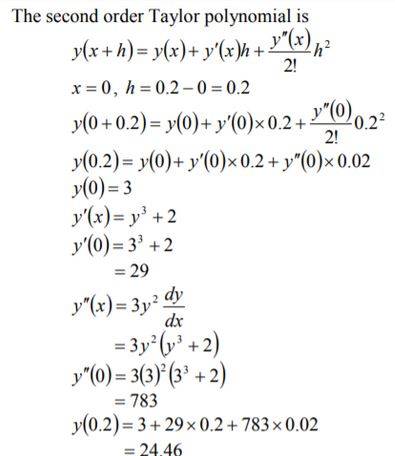- What is Taylor series?
- Weightage of Taylor's Series
- Illustrated Examples on Taylor's Series
- FAQ on Taylor's Series
What is Taylor series?
The Taylor series is the most famous series used in several mathematical and practical problems. Taylor's theorem expresses a function in the form of the sum of the infinite terms. These terms are determined from the derivative of a given function for a particular point. The standard definition of an algebraic function is provided using an algebraic equation. Similarly, transcendental functions are defined as a property that holds them. Its Taylor series can also describe a function. This series can also be used to determine various functions in many fields of mathematics.
Taylor's Series Theorem
Suppose if f (x) is a real or composite function, which is a different function of a district number also real or composite. Then the Taylor series describes the following series of powers:
f(x) = f(a)f′(a)1!(x−a) + f"(a)2!(x−a)2 + f(3)(a)3!(x−a)3 + …
The Taylor arrangement can consist of
∑∞n = 0fn(a)n!(x−a)n
Where,
f(n) (a) = nth subsidiary of f
n! = factorial of n
Taylor Series Formula
We know that the power series can be defined as
f(x) = ∑∞n = 0anxn = a0 + a1x + a2x2 + a3x3 + …
At the point when x = 0,
f(x) = a0
Along these lines, by separating the given capacity, it becomes,
f'(x) = a1 + 2a2x + 3a3x2 + 4a4x3 + …
Once more, when we substitute x = 0, we get,
f'(0) = a1
Thus, separating it once more, we get,
f"(x) = 2a2 + 6a3x + 12a4x2 + …
Now, replacing x = 0 in the second-order differentiation, we get
f"(0) = 2a2
In this manner, [f"(0)/2!] = a2
By summing up the condition, we get,
f n (0)/n! = an
Now replace the values of the series of powers we get,
f(x) = f(0) + f′(0)x + f"(0)/2! (x2 )+ f"'(0)/3! (x3 )+ …
Generalise f of more general shape, it becomes
f(x) = b + b1 (x-a) + b2( x-a)2 + b3 (x-a)3 + …
x = a, we get
bn = fn(a)/n!
Substituting bn in a summed up structure
f(x) = f(a)f′(a)1!(x−a) + f"(a)/2!(x−a)2 + f(3)/(a)3!(x−a)3 + …
Thus, this is the Taylor theorem.
Weightage of Taylor's Series
In this chapter 'Sequence and Series', this chapter has discussed the Taylor series in detail with it and the theorem, along with various parts of it has been briefly cleaned. This chapter weighs 30 marks.
Illustrated Examples on Taylor's Series
1.What will be the coefficient for the term x5 term in the Maclaurin polynomial for sin(2x)?
Solution.
2. Given f (3) = 6, f ′(3) = 8, f ′′(3) = 11, and any remaining higher request subordinates of f (x) are zero at x = 3, and expecting the capacity and every one of its subsidiaries exists and are persistent between x = 3 and x = 7, the estimation of f (7) is?
Solution.
3. Given that y(x) is the answer for 2 3 = y + dx dy, y(0) = 3 the estimation of y(0.2) from a second request Taylor polynomial around x=0 is?
Solution.
FAQ on Taylor's Series
Q: What are some applications of the Taylor series?
Q: What will be the Taylor series for sin x?
Q: What is the general term for the Taylor series?
Q: In the Taylor series, what will be its first-degree polynomial?
Q: Can we say that zero is a polynomial?
Maths Sequence and Series Exam
Student Forum
Popular Courses After 12th
Exams accepted
CA FoundationExams accepted
ICSI ExamExams accepted
BHU UET | GLAET | GD Goenka TestBachelor of Business Administration & Bachelor of Law
Exams accepted
CLAT | LSAT India | AIBEExams accepted
IPMAT | NMIMS - NPAT | SET
Exams accepted
BHU UET | KUK Entrance Exam | JMI Entrance ExamBachelor of Design in Animation (BDes)
Exams accepted
UCEED | NIFT Entrance Exam | NID Entrance ExamBA LLB (Bachelor of Arts + Bachelor of Laws)
Exams accepted
CLAT | AILET | LSAT IndiaBachelor of Journalism & Mass Communication (BJMC)
Exams accepted
LUACMAT | SRMHCAT | GD Goenka Test