Parabola Graph: Overview, Questions, Preparation

A parabola is a curve whose equation is f(x)= ax²+bx+c, which is the normal form of a parabola. To draw a parabola, we need to define the vertex first. This can be achieved by solving the equation x=-b/2a, and then having y= f (-b/2a) Plotting the graph, where the quadratic equation is given in the form of f(x) = a (x-h)² + k, where (a, k) is the vertex of the parabola, is its vertex form. Find the vertex, focus, and directrix for a parabola here. 

We know f(x) = ax² + bx + c and a, b and c are constants, while x is the vector. By locating the values of x and y or by f(x), we will plot all the points in the graph, and by joining them, we will get the appropriate form. Later, we can create and graph a parabola.

How to graph a parabola?

Two points will describe a line. We have to find more than two points for the parabola to map it. We need to decide on five key points for a design that would be aesthetically pleasing. To begin our parabola, we start by inputting the details. 

Suppose we have a quadratic equation of the form y=ax² + bx + c , where a, b, and c are variable. To evaluate the values of x, you have to find the y-values. Now, the values of x and y will take us to the position of the point where the required parabola intersects the y-axis. By using these points and the X-axis, we can draw a line.

This concept is taught under the chapter Conic Sections. You will learn about the parabolic graph and its applications in plotting equations. The weightage of this chapter is 4-7 marks in the final exams.

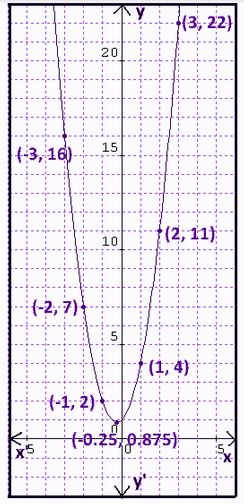
1. Draw a graph for the equation y = 2x² + x+ 1.
Solution. The given equation is y = 2x² + x+ 1.
Here, a = 2, b = 1 and c = 1.
It needs to find the vertex now
x = -b/(2a)
x = -1/(2(2))
x = -1/ 4
x = -0.25
Now putting x = -0.25 in the equation y= 2x² + x+ 1
y= 2(-0.25)² + (-0.25)+ 1.
y = 2(0.0625) – 0.25+1
y = 0.125 – 0.25 +1
y = 0.875
Now putting the different values for x and calculate the corresponding values for y.
When x = 1 ⇒ y= 2x² + x+ 1 ⇒ y = 2(1)²+ 1 + 1 ⇒ y = 2+ 1 + 1 ⇒ y = 4
When x = 2 ⇒ y= 2x² + x+ 1 ⇒ y = 2(2)²+ 2 + 1 ⇒ y = 8+ 2 + 1 ⇒ y = 11
When x = 3 ⇒ y= 2x² + x+ 1 ⇒ y = 2(3)²+ 3 + 1 ⇒ y = 18+ 3 + 1 ⇒ y = 22
When x = -1 ⇒ y= 2x²+ x+ 1 ⇒ y = 2(-1)²– 1 + 1 ⇒ y = 2- 1 + 1 ⇒ y = 2
When x = -2 ⇒ y=2x²+ x+ 1 ⇒ y = 2(-2)²– 2 + 1 ⇒ y = 8- 2 + 1 ⇒ y = 7
When x = -3 ⇒ y= 2x² + x+ 1 ⇒ y = 2(-3)²– 3 + 1 ⇒ y = 18 -3 + 1 ⇒ y = 16

Hence,

Q: What is a parabola?

Q: What is the primary property of parabola?

Q: What are some examples of parabolas? Why are they useful?

Q: Write differences between hyperbola and parabola.

Q: What are parabolas used for?