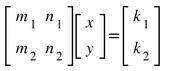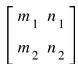Rachit Kumar SaxenaManager-Editorial
What is Jacobian?
A matrix is a form of representation of a pair of linear equations. The coefficients of a variable are structured in a box format to form a matrix. For a system of linear equations,
m1x+ n1y =k1 and m2x+ n2y =k2, the matrix representation is:
For a unique solution, the condition is m1n2- m2 n1 ≠0. This equation is represented in the form of a matrix,
The determinant of a matrix of partial derivatives is known as the ‘Jacobian’.
Jacobian Method
The method that is used to determine the solutions of a system of linear equations is known as the Jacobian method. It is an iterative algorithm where the diagonal elements of a matrix are assigned an approximate value. Then, the matrix is solved to reach convergence, and this process of matrix diagonalisation is known as the Jacobi transformation.
Consider a matrix M for the ‘n’ system of linear equations.
Then, Mx = N
m11 m12 .............m1n
m22 m23 .............m2n
... ... ... ...
mn1, mn2, ... mnn
x= x1, x2 ....xn
p= p1, p2 ....pn
Decompose the matrix M into the diagonal component ‘D’ and remainder ‘R’ such that M= D+ R.
D=
m11 0 ... 0
0 m22 ... 0
... .... ....
0 0 ....... mmn
R=
0 m12 ... m1n
m22 0 ... m2n
... ..... ....
mn1 mn2 ....... 0
So, the solution for these equations can be denoted as:
x(s+1) = D-1 (b- Rxs),
Where xs is the sth iteration or approximation of s. Also, xs+1 is the (s+1)th iteration of x or the next iteration after xs.
id="" class="figure"
Weightage of Jacobian in Class 12
Illustrative Example on Jacobian
1. Using the Jacobian method, find the solution of the system of linear equations:
2x + 5y = 1 and 3x + 2y = 7.
Solution:
These equations can be written in the form:
MX= N
Where M=
(2 5)
(3 2)
X= (x)
(y)
N= (1)
(7)
Now, |M|= -11 ≠ 0.So M is a nonsingular matrix and has a unique solution.
M-1 = (1/11)
(2 5)
(3 2)
X= M-1 . N
X= (1/11)
(2 5)
(3 2)
(1/7)
Which means, X= (3, 1)
Hence, x= 3 and y= -1.
2. Find the Jacobian for the equations:
p1= (3m+n+1)2, p2= (mn+2m+3n) for m=n=0.
Solution:
For p1= (3m+n+1)2, p2= (mn+2m+3n),
We know that, m=n=0.
Also, 6(3m+n+1) at m=n=0 is 6
2(3m+n+1) is 2
(n+2+0)= 2
(m+0+3)= 3
So, J(p1,p2)= (6, 2)
(2, 3)
3.Let x (m, n) = m2 – n2 , y (m, n) = 2 mn. Find the Jacobian J (m, n).
Solution:
Given that, x(m,n)= m2- n2 and y(m,n)= 2mn
So, J(m,n)= 4m2+4n2
4. Solve the following system of equations by matrix method.
3x – 2y + 3z =8, 2x + y – z =1, 4x – 3y + 2z =4.
Solution:
The system of linear equations can be represented as
MX= N
So, |M|= 3(2 -3)+ 2(4+ 4)+ 3(-6 -4)= -17 0.
X= M-1.N
-34 2
-51} 3}
Hence, x= 1, y=2, and z=3.
FAQs on Jacobian
Q: What is a matrix?
Q: What is a determinant?
Q: What is a minor and a cofactor?
Q: What are the methods to solve a system of linear equations?
Q: What are the applications of matrices and determinants?
News & Updates
Determinants Exam
Student Forum
Popular Courses After 12th
Exams: BHU UET | KUK Entrance Exam | JMI Entrance Exam
Bachelor of Design in Animation (BDes)
Exams: UCEED | NIFT Entrance Exam | NID Entrance Exam
BA LLB (Bachelor of Arts + Bachelor of Laws)
Exams: CLAT | AILET | LSAT India
Bachelor of Journalism & Mass Communication (BJMC)
Exams: LUACMAT | SRMHCAT | GD Goenka Test