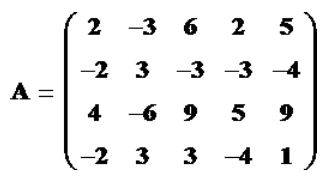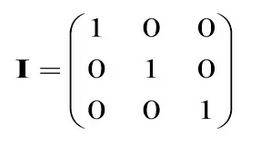Identity Matrix: Overview, Questions, Preparation

The identity matrix has many names; it is also called the unit matrix or the elementary matrix. It is a matrix wherein the diagonal has ones, and the other matrix members are 0. It is an n x n square matrix represented by the letter ‘I’. It is one of the types of diagonal matrices. We will discuss its definition and properties along with some illustrated examples.

An identity matrix is defined as a diagonal square matrix where the diagonal members are 1, and the rest are 0. It is represented by I or I with a subscript n. Whenever you multiply any matrix by the identity matrix, the result will be the matrix itself; it will be discussed under the properties as well.

Properties of an Identity Matrix

• The identity matrix is always square. These matrices always have the same number of rows and columns, and they are said to be square matrices. For any rational number ‘n’ the corresponding matrix will be n x n.
• Any matrix ‘a’ multiplied by the identity matrix gives the matrix ‘a’ itself.
• The size of the matrix matters a lot when we are multiplying it. For any matrix when we have to multiply m x n, the matrix’s size is very important. ImC=C=CIn.
• When any two inverse matrices are multiplied, the matrix obtained is an identity matrix.
• Whenever we multiply two matrices that are inverse of each other, then the resultant matrix that we obtain is an identity matrix.

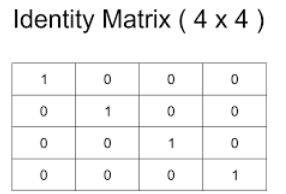
1. Give an example of a 4x4 unit or elementary or identity matrix.

Solution.

Since it is an identity matrix, there have to be the diagonals having 1 as the unit members and the other elements of the matrix can be 0.

2.Check if the following matrix is an identity matrix or not.

Solution.

The above-listed matrix is not an identity matrix since it does not have 1 and 0 as its elements.

3.Check if the following matrix is an identity matrix or not.

Solution.

The above-listed matrix is an identity matrix since it has 1 in its diagonals and 0 as the elements and because it is a square matrix.

Q: What is an identity matrix?

Q: What type of matrix is it?

Q: What are the properties of an identity matrix?

Q: What are the other names of the identity matrix?

Q: What happens when two inverse matrices are multiplied?