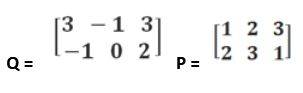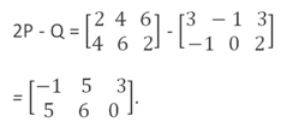- What is Algebra of Matrices?
- Weightage of Algebra of Matrix
- FAQs on Algebra of Matrices
What is Algebra of Matrices?
A matrix is the arrangement of numbers in a rectangular array that includes horizontal rows and vertical columns. Algebra of matrices involves certain tasks performed over one or more than one matrices like multiplication, addition, subtraction, etc.
Let us have a look at these operations.
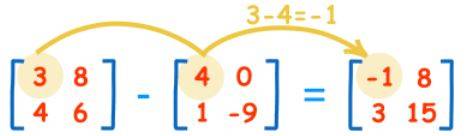
1. Addition/Subtraction of Matrices: Operation of addition or subtraction of matrices is possible only if both the matrices have the same number of columns and rows.
3. Multiplication with Another Matrix: This type of multiplication is possible between two matrices only when the number of the first matrix's column and the number of the second matrix's row are equal.
Standards of Matrix Algebra
- Commutative Law of Addition: P + Q = Q + P.
- Associative Law of Addition: P + Q + R = P + (Q + R) = (P + Q) + R.
- Associative Law of Multiplication: P(QR) = (PQ)R.
- R(P+Q) = RP + RQ, here R = Real Number.
Standards for the Inverse of Matrices
PI = IP = P
PP-1 = P-1P = I
(P-1)-1 = P
(PQ)-1 = Q-1P-1
(PQR)-1 = R-1Q-1P-1
(PT)-1 = (P-1)T
Standards for Matrices' Transportation
- (PT)T = P
- (P+Q)T = PT+QT
- (PQ)T = QTPT
(PQR)T = RTQTPT
Weightage of Algebra of Matrix
Matrix is an important chapter from the point of view of class XII exams and other competitive exams. Algebra of matrices is also a part of this chapter; the chapter's weightage ranges from 8 to 10 marks in class XII exams. Algebra of matrices covers the various operations performed on matrices. Apart from that, the other crucial topics included in the chapter are:
- Symmetric matrices
- Skew-symmetric matrices
- Transformation of matrices
- Finding the inverse of a matrix
Illustrated Examples on Algebra of Matrix
1.Find the value of 2P - Q matrix, where
Applying operation on P and Q,
2. Find p and q, if
Therefore, we obtain from the above equation that,
2p+3 = 7 and q-1 = 14,
p = 2, q = 9.
3. If
FAQs on Algebra of Matrices
Q: Is it possible to multiply two matrices, provided the number of columns of the first matrix is different from the number of rows of the second matrix?
Q: What will we get if we multiply the matrix with an identity matrix?
Q: What will be the resultant matrix's order if the order of the matrix is m1*n1 and matrix two is m2*n2, where n1 = m1?
Q: Where are the matrices used in daily life?
Business and Economics
Construction
Animation, etc.
Q: What is a row matrix?
Maths Matrices and Determinants Exam
Student Forum
Popular Courses After 12th
Exams accepted
CA FoundationExams accepted
ICSI ExamExams accepted
BHU UET | GLAET | GD Goenka TestBachelor of Business Administration & Bachelor of Law
Exams accepted
CLAT | LSAT India | AIBEExams accepted
IPMAT | NMIMS - NPAT | SET
Exams accepted
BHU UET | KUK Entrance Exam | JMI Entrance ExamBachelor of Design in Animation (BDes)
Exams accepted
UCEED | NIFT Entrance Exam | NID Entrance ExamBA LLB (Bachelor of Arts + Bachelor of Laws)
Exams accepted
CLAT | AILET | LSAT IndiaBachelor of Journalism & Mass Communication (BJMC)
Exams accepted
LUACMAT | SRMHCAT | GD Goenka Test