- What is Inverse Matrix?
- Find Inverse of Matrix
- Weightage of Inverse of Matrix
- Illustrated Examples on Inverse of Matrix
- FAQs on Inverse Matrix
What is Inverse Matrix?
A matrix is a definite set of objects organised in columns and rows. These objects are referred to as matrix components. The order of a matrix is entered by the number of rows compared to the number of columns.
The inverse of a matrix:
If A is a non-singular square matrix, n x n matrix A-1 exists, which is called the inverse matrix of A in such a way that the property is satisfied:
A.A-1 = A-1. A = I, where the matrix of identity is I.
An important condition: The square matrix can be non-singular to find the opposite matrix, the determinant value of which is not equal to zero.
Find Inverse of Matrix
When numbers are written in rows and columns, they form a matrix. The order of the matrix is represented as the number of rows by the number of columns. For example, 2 × 2, 2 × 3, 3 × 2, 3 × 3, 4 × 4 etc.
However, the inverse of a matrix may be found when the specific matrix is a square matrix. A square matrix is a matrix whose number of columns and rows are equal, such as 2 × 2, 3 × 3, etc. To find the inverse of the matrix, the square matrix must be non-singular whose determinant value does not equal zero.
Methods to Find the Inverse Matrix
There are three different methods to find the inverse of a matrix.
- Using determinants.
- Using minors and cofactors of elements.
- Elementary Transformation.
There are mainly two ways to find an inverse of a matrix:
1. Determinant method:
To find the inverse of a matrix, by the determinant method, you should know how to calculate adjoint and the determinant of the matrix.
The inverse of the matrix is given by - 1/|determinant|. adj(A)... where A is the matrix
2. Elementary transformation method:
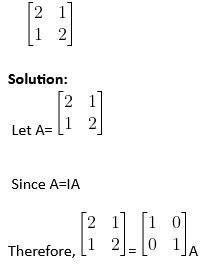
For finding the matrix by the elementary transformation method, we have to convert the matrix first into an identity matrix. After that, write A = IA, where the identity matrix of the same order as A is I. Apply a row operation sequence before we have an identity matrix on the LHS and use the same elementary RHS operations to get I = BA. Matrix B on the RHS is matrix A's inverse. Write A = IA and apply column operations sequentially until I = AB is obtained, where B is the inverse matrix of A, to find the inverse of A using column operations.
Properties of Inverse of the Matrix:
The properties of inverse matrices are listed below.
If A and B are nonsingular matrices, then the inverse matrix will have the following properties:
- (A-1)-1 = A
- (AB)-1 = A-1B-1
- (ABC)-1 = C-1B-1A-1
- (A1 A2….An)-1 = An-1An-1-1……A2-1A1-1
- (AT)-1 = (A-1)T
- (kA)-1 = (1/k) A-1
Weightage of Inverse of Matrix
In the chapter ‘Matrix,’ you will learn about the inverse matrix and the different methods associated with it. The weightage of this chapter is 6-7 marks. The topic of the inverse of a matrix is covered in the chapter Matrices. The students get to learn about the fundamentals of matrix and matrix algebra. The chapter has a weightage of 13 marks.
Illustrated Examples on Inverse of Matrix
1. Find the inverse of the matrix:
A=
| 1 2 3 5 |
Solution:
Determinant = -1≠0 .. means inverse is possible
Now we have to calculate the adjoint .. the adjoint matrix is equal to:
| 5 -2 -3 1 |
This is the adjoint matrix we get
So the inverse of the matrix is given by:
A-1 = 1/|determinant|. Adj (A)
=
| -5 2 3 -1 |
2. Find the inverse of the matrix:
| 2 1 7 4 |
Solution: The determinant of the matrix is = 1, so the inverse of the matrix is possible
Adjoint of the matrix =
| 4 -1 -7 2 |
The inverse of the matrix =
| 4 -1 -7 2 |
3. What is the inverse of
| 5 6 -1 2 |
Solution:
A−1 =
1/det x
| 5 6 -1 2 |
| 2 -6 -1(-1) 5 |
Since determinant
| 5 6 -1 2 |
=16
Therefore, A−1=1/16
| 2 -6 -1(-1) 5 |
=
| 1/8 -3/8 1/16 5/16 |
4. Matrices A and B will be inverse of each other only if
(A) AB = BA (B) AB = BA = 0 (C) AB = 0, BA = I (D) AB = BA = I
Solution:
Option (A) AB = BA is correct.
5. Find the inverse of the matrix if it exists.
FAQs on Inverse Matrix
Q: How can the opposite of the matrix be found?
Q: How can you find a 3x3 matrix inverse?
2: Then transform it into the cofactors matrix;
3: The adjugate, then;
4: Multiply 1/determinant by that.
Q: What is a matrix’s right inverse?
Q: What is the inverse of the identity matrix?
Q: What is the cofactor matrix?
Q: What's going to happen when you reverse the matrix?
Q: Is the reciprocal of the matrix invertible?
Q: Is the inverse or reversal of the matrix unique?
Q: What can be the result when it is inverted?
Q: Has inverse of a matrix commutative nature?
Maths Matrices and Determinants Exam
Student Forum
Popular Courses After 12th
Exams accepted
CA FoundationExams accepted
ICSI ExamExams accepted
BHU UET | GLAET | GD Goenka TestBachelor of Business Administration & Bachelor of Law
Exams accepted
CLAT | LSAT India | AIBEExams accepted
IPMAT | NMIMS - NPAT | SET
Exams accepted
BHU UET | KUK Entrance Exam | JMI Entrance ExamBachelor of Design in Animation (BDes)
Exams accepted
UCEED | NIFT Entrance Exam | NID Entrance ExamBA LLB (Bachelor of Arts + Bachelor of Laws)
Exams accepted
CLAT | AILET | LSAT IndiaBachelor of Journalism & Mass Communication (BJMC)
Exams accepted
LUACMAT | SRMHCAT | GD Goenka Test