Sec 30: Overview, Questions, Preparation

In trigonometry, you might have heard the three major primary functions, such as sine, cosine, and tangent, along with the other three trigonometric functions, such as secant, cotangent, and cosecant. Here you can find the value of 30 degrees sec along with the other values of the secant degree. 

The transposing function of the cosine is a secant function. Therefore, in order to find the value of sec 30, we need to find the value of cos 30. We use the relation of the right-angle triangle to derive the values of trigonometric functions or ratios such as sin, cos, tan, sec, cot, cosec. 

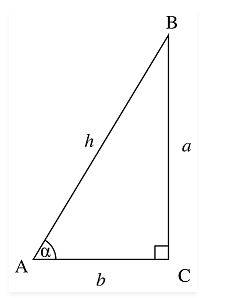
As we know, the Cosine equation determines the relationship between the adjacent side and the hypotenuse of the right-angled triangle with respect to the angle formed between the adjacent side and the hypotenuse. Thus, we can assume that the secant function determines the relationship between the hypotenuse and the adjacent side of the right-angled triangle with respect to the angle developed between the adjacent side and the hypotenuse. Thus, the ratio of the hypotenuse to the adjacent side would be Sec 30. 

With the aid of the cos function, we can obtain the value of sec 30 degrees. Even values in other degrees, such as 0, 45, 60, 90 which are commonly found in trigonometric equations. 

We realise that, in the right-angled triangle, the secant of the axle is the ratio of the length of the axle and the opposing side to the angle where the axle is formed between the adjacent side and the axle. 

secant ∠α = Hypotenuse/Adjacent Side

= Hypotenuse/Base

sec ∠α = h/b

Now, sec ∠α = 1/cos ∠α

Therefore, sec 30 = 1/cos 30

The value of cos 30 = √3/2

Hence, the value of sec 30 = 2/√3

Sec 30 degrees in Class 10

In this class, there are only the basics of trigonometry. Here you will get to learn about the value and theorem of the basic angle of secant as well as other ratios.

Sec 30 degrees in Class 11

Discussion of trigonometry is in detail in Class 11. In different chapters, you will get to learn about the basic values as well as values in all the coordinates. The weightage of trigonometry is 22 marks in the examination.

Sec 30 degrees in Class 12

Application of trigonometry is there in detail about the secant and other angles and its use in calculus and other branches. The weightage of trigonometry is 5-6 marks.

Compute 2 sec 30 + 2 cos 60.

Solution:

Given,

2 sec 30 + 2 cos 60

We know, sec 30 = 2/√3 and cos 60 = ½

Therefore,

2 sec 30 + 2 cos 60 = 2 × 2/√3 + 2 × ½

= 4/√3 + 1

2 sec 30 + 2 cos 60= 4/√3 + 1.

Solve cos 30 . sec 30- sec2 30

Solution:

3/2 . 2/3- (3/2)2 = ¼

Q: What is equal to the SEC?

Q: Is Sec 1 the same thing as Cos?

Q: What's SEC in trigonometry?

Q: How to solve sec?

Q: What is the meaning of sec theta?