- Applications of Trigonometry
- Heights and Distances
- Illustrative Examples
- Frequently Asked Questions
Applications of Trigonometry
Although trigonometry was first developed for astronomy, trigonometry later found its way into cartography, aviation and naval industries, construction, and believe it or not, even in music. Trigonometry has many applications in calculating heights and distances such as the height of towers or mountains, distance of shore from the sea, distance between stars, and so on.
Heights and Distances
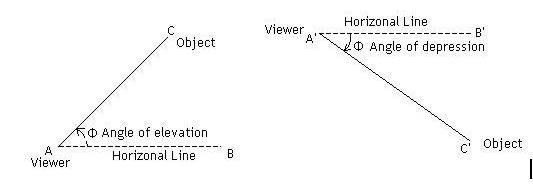
This concept is one of the main trigonometry applications. A right-angled triangle can always be formed from the line of sight and the angle of elevation or depression, using the horizontal level as a base.
The angle of elevation is the angle formed by the line of sight and horizontal level, where the object viewed is above the base; i.e., we have to look up.
The angle of depression is the angle formed where the object viewed is below the base; i.e., we have to look down.
Given the angle at any one distance, all others can be calculated with ease by using the trigonometric ratios.
About the Topic
Applications of Trigonometry are introduced to students in the 10th grade. In the CBSE 10th Mathematics board exam, this chapter has a weightage of 12 marks. Ample knowledge of trigonometry is necessary to understand Maths and Physics in higher classes.
Illustrative Examples
1. A circus artist is climbing a 20m long rope, which is tightly stretched and tied from the top of a vertical pole to the ground. Find the height of the pole if the angle made by the rope with the ground level is 30°.
First and foremost, let us start with the diagram and the given information.
The length of the rope, AC=20m and ∠ACB=30°.
Assume, the height of the pole= h meters.
Then, sin(30°)= AB/AC.
We know, sin(30°)=½
∴1/2 = AB/AC
12=h20
∴h =10m
Hence, the height of the pole =10m.
2. The angle of elevation of the top of the tower from a point on the ground, which is 30m away from the tower’s foot, is 30°. Find the height of the tower.
Assume ‘h’ is the height of the tower.
In ∆ABC,
AB/BC = tan(30°)
I.e, h30=1√3
∴h=30√3
=30√3X√3√3= 10√3m.
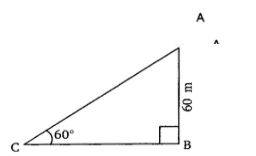
3. A kite is flying at a height of 60m above the ground. The string attached to the kite is temporarily tied to a point on the ground. The inclination of the string with the ground is 60°. Find the length of the string, assuming that there is no slack in the string.
In ∆ABC,
AB=60m and ∠ACB=60°.
Let the length of the string be= AC.
Then, sin(60°)=ABAC
√32= 60AC
AC=602333=12033=403m.
Hence, the length of the string is 403m.
Frequently Asked Questions
Q: What are trigonometric ratios?
- sin(θ) = opposite/hypotenuse
- cos(θ) = adjacent/hypotenuse
- tan(θ) = opposite/adjacent
- cosec(θ) = hypotenuse/opposite
- sec(θ) = hypotenuse/adjacent
- cot(θ) = adjacent/opposite
Q: How is trigonometry useful?
Q: Which fields make use of applications of trigonometry other than mathematics?
Q: If the distance of a pillar from the viewer and the pillar’s height is equal, what is the angle of elevation?
Q: If the length of the imaginary triangle’s hypotenuse is known and the base, which trigonometric ratio is used to calculate the angle?
Maths Trigonometry Exam
Student Forum
Popular Courses After 12th
Exams accepted
CA FoundationExams accepted
ICSI ExamExams accepted
BHU UET | GLAET | GD Goenka TestBachelor of Business Administration & Bachelor of Law
Exams accepted
CLAT | LSAT India | AIBEExams accepted
IPMAT | NMIMS - NPAT | SET
Exams accepted
BHU UET | KUK Entrance Exam | JMI Entrance ExamBachelor of Design in Animation (BDes)
Exams accepted
UCEED | NIFT Entrance Exam | NID Entrance ExamBA LLB (Bachelor of Arts + Bachelor of Laws)
Exams accepted
CLAT | AILET | LSAT IndiaBachelor of Journalism & Mass Communication (BJMC)
Exams accepted
LUACMAT | SRMHCAT | GD Goenka Test