- Sec 60
- Finding the value of Sec 60
- Illustrated Examples
- Frequently Asked Questions
Sec 60
In mathematics, we know that a right angle triangle has three sides and three angles. Among those three angles, one angle is 90°, and the three sides are Hypotenuse, Perpendicular, and Base. The ratio of the hypotenuse and the base are known as the secant of the angle. Suppose we have angle θ in the right-angled triangle, then the secant for θ will be
sec θ = Hypotenuse/Base
sec θ is the reciprocal of cos θ hence it can also be written as 1/cos θ.
Finding the value of Sec 60
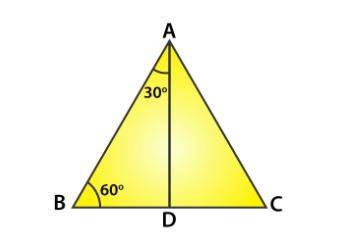
For finding the value of sec 60°, we are considering an equilateral triangle ABC. Therefore every angle will be 60°( ∠A=∠ B=∠ C=60°).
Now, from A, we will draw a perpendicular line AD at BC
Therefore △ ABD ≅ △ACD and BD = DC,
If BD = DC then ∠ BAD = ∠ CAD = 30°,
Now, let us assume the lengths of each side to be 2a,
Therefore AB = BC = CA = 2a and BD = DC = a,
Now we'll find the value of cos 60°,
cos θ = 1/sec θ = Adjacent Side / Hypotenuse
Now θ = 60°
Cos 60°= BD/AB = a/2a
Hence cos 60° = 1/2,
Now, we know that the reciprocal of cosine is secant
Therefore sec 60° = 1/cos 60° = 2.
Secant is the trigonometry angle; apart from that, there are also other trigonometric operators like sin, cos, cot, tan, cosec. The trigonometric values from 0 to 90 are:
| Θ = |
sin θ |
cosec θ |
cos θ |
sec θ |
tan θ |
cot θ |
|---|---|---|---|---|---|---|
| 0 |
0 |
Not Defined |
1 |
1 |
0 |
Not Defined |
| 30 |
1/2 |
2 |
√3/2 |
2/√3 |
1/√3 |
√3 |
| 45 |
1/√2 |
√2 |
1/√2 |
√2 |
1 |
1 |
| 60 |
√3/2 |
2/√3 |
1/2 |
2 |
√3 |
1/√3 |
| 90 |
1 |
1 |
0 |
Not Defined |
Not Defined |
0 |
Secant is the topic of the chapter Introduction to Trigonometry of class X mathematics. The chapter is involved in various fields of mathematics. Every year around 5 to 6 questions ranging from easy to moderate level are asked from the chapter. The weightage of these questions in class X exams is 10 to 12 marks. Introduction to trigonometry also includes topics like:
- Trigonometric Ratios of complementary and specific angles
- Trigonometric Identities
- Measurement of height and distances using trigonometric applications
Illustrated Examples
1. Suppose in a right-angled triangle the XYZ, the base's length is 21cm and Hypotenuse's length is 29 cm. Then find the value of cos2 + sin2?
From applying the Pythagoras theorem, we will get the perpendicular's length, i.e., 20cm.
Now cosθ = 21/29 and sinθ = 20/29,
Therefore cos2 + sin2 = (21/29)2 + (20/29)2 = 1.
2. Write cot 85° + cos 75° in the manner of 0° to 45°.
We know that cot θ can be written as tan(90- θ) and cos θ as sin(90- θ).
Therefore, cot 85° + cos 75° = tan(90-85) + sin(90-75)
= tan 5° + sin 15°.
3. Prove that sec θ (sec θ + tan θ) (1 -sin θ) = 1.
Taking LHS,
sec θ(1 -sin θ)(sec θ + tan θ)
= (1/cos θ)*(1/cos θ + sinθ/cos θ)*(1-sin θ)
= (1+sinθ)*(1-sin θ)/cos2 θ
= (1-sin2 θ)/cos2 θ
= 1.
Frequently Asked Questions
Q1. What is the reciprocal of tan θ?
Q2. Mention the undefined trigonometric angles from the first quadrant?
- tan 90°
- cot 0°
- cosec 0°
- sec 90°
Q3. cos A + cos B equals to?
Q4. What is the value of sec 15?
Q5. Write sec θ in the manner of cosec?
Maths Trigonometry Exam
Student Forum
Popular Courses After 12th
Exams accepted
CA FoundationExams accepted
ICSI ExamExams accepted
BHU UET | GLAET | GD Goenka TestBachelor of Business Administration & Bachelor of Law
Exams accepted
CLAT | LSAT India | AIBEExams accepted
IPMAT | NMIMS - NPAT | SET
Exams accepted
BHU UET | KUK Entrance Exam | JMI Entrance ExamBachelor of Design in Animation (BDes)
Exams accepted
UCEED | NIFT Entrance Exam | NID Entrance ExamBA LLB (Bachelor of Arts + Bachelor of Laws)
Exams accepted
CLAT | AILET | LSAT IndiaBachelor of Journalism & Mass Communication (BJMC)
Exams accepted
LUACMAT | SRMHCAT | GD Goenka Test