- Cos Meaning
- The Formula of Cos
- The Table of Cos
- Identities of Cos
- Importance and Weightage
- Illustrated Examples
- FAQs on Cos Meaning
Cos Meaning
The cos, in mathematics, refers to the cosine function, which is the very basic part of trigonometry. There are three main functions of trigonometry, which are: sine, cosine and tangent. Cos is one of the main functions of trigonometry. It is defined as the ratio between the lengths of sides and the hypotenuse. Cosine helps in finding the length and angles of various triangles.
The Formula of Cos
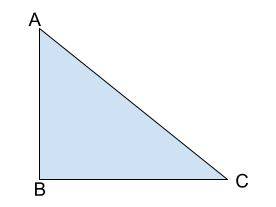
Suppose we have a triangle named ABC.
For angle C in the given triangle ABC, the formula of cos is:
cos C = base / hypotenuse = BC / AC
(Here, AC is the hypotenuse, AB is the perpendicular, and BC is the base.)
Similarly, for angle A in triangle ABC, cos will be written as:
cos A = base/hypotenuse = AB/AC
(Here, BC acts as the perpendicular, AB as the base, and AC as the hypotenuse)
Therefore, the general formula of cos is:
cosӨ = adjacent side to angle Ө/hypotenuse
The Table of Cos
We can derive many values of cos. But some of the basic values that are required to solve questions are 0°, 30°, 45°, 60°, 90°, etc. These help us find angles and solve the question further. You can easily learn these values as given below:
cos 0° = 1
cos 30° = 3/ 2
cos 45° = 1/2
cos 60° = 1/2
cos 90° = 0
cos 120° = -1/2
cos 150° = -3/ 2
cos 180° = -1
cos 270° = 0
cos 360° = 1
Identities of Cos
Identities are essential when it comes to solving trigonometric equations. Some basic and important identities of cos are as follows:
cos2Ө + sin2Ө = 1
cos Ө = 1/sec Ө
cos (−Ө) = cos (Ө)
arccos ( cos ( Ө ) ) = Ө + 2kӨ (where k is an integer)
Cos (2Ө) = cos2 (Ө) − sin2 (Ө)
cos (Ө) = sin (π/2 − Ө)
Importance and Weightage
This chapter holds the basic knowledge of the concepts of trigonometry. It is important to learn this chapter with attention as the level of difficulty increases in classes 11 and 12. The chapter carries 12 marks in your class 10 board exams.
Illustrated Examples
1. In triangle OPQ, right-angled at P, OP = 7 cm and OQ – PQ = 1 cm (see Fig.). Determine the values of sin Q and cos Q.
source:ncert
Solution: In triangle OPQ,
OQ2 =OP2 +PQ2
(1 + PQ)2 = OP2 +PQ2
1 +PQ2 +2PQ=OP2 +PQ2
1+2PQ = 7*7
2PQ = 48
PQ = 24
Therefore, OQ = 1 + PQ
OQ = 1 +24= 25
Thus, sin Q = OP/OQ
Sin Q= 7/25
And cos Q = PQ/OQ
Cos Q= 24/25
2. Express the ratios cos A, tan A and sec A in terms of sin A.
Solution: We know that cos2A+ sin2A= 1
cos2A= 1 -sin2A
cosA= 1 -sin2A
tan A = sin A/cos A
tan A = sin A/1 -sin2A
sec A = 1/cos A = 1 /1 -sin2A
3. If sin 3A = cos (A – 26°), where 3A is an acute angle, find the value of A.
Solution : Since sin 3A = cos (90° - 3A)
Therefore, cos ( 90° - 3A) = cos (A - 26°)
90° - 3A = A - 26°
90° + 26° = A + 3A
4A = 116
A = 116/4
A = 29°
Q: What is the unit of cos?
A: Cos is a ratio and ratios do not have any unit.
Q: What is the reciprocal of cos?
A: The reciprocal relation of cos is written as cos Ө = 1/sec Ө
Q: State all the types of trigonometric functions.
A: sin = opposite/hypotenuse
cos = adjacent/hypotenuse
tan = opposite/adjacent
cot = adjacent/opposite
cosec = hypotenuse/opposite
sec = hypotenuse/adjacent
Q: Write tan in terms of cos.
A: tan Ө = sin Ө/cos Ө
Q: What is the maximum possible value of cos?
A: 1
FAQs on Cos Meaning
Maths Trigonometry Exam
Student Forum
Popular Courses After 12th
Exams accepted
CA FoundationExams accepted
ICSI ExamExams accepted
BHU UET | GLAET | GD Goenka TestBachelor of Business Administration & Bachelor of Law
Exams accepted
CLAT | LSAT India | AIBEExams accepted
IPMAT | NMIMS - NPAT | SET
Exams accepted
BHU UET | KUK Entrance Exam | JMI Entrance ExamBachelor of Design in Animation (BDes)
Exams accepted
UCEED | NIFT Entrance Exam | NID Entrance ExamBA LLB (Bachelor of Arts + Bachelor of Laws)
Exams accepted
CLAT | AILET | LSAT IndiaBachelor of Journalism & Mass Communication (BJMC)
Exams accepted
LUACMAT | SRMHCAT | GD Goenka Test