- What Are Trigonometry Values?
- Applicability of Trigonometry
- Illustrated Examples
- Frequently Asked Questions
What Are Trigonometry Values?
These are the values of standard angles of a triangle. These values are based on Trigonometry functions like Sine, Cosine and Tangent called the primary functions and Cosecant, Secant, and Cotangent called the secondary functions.
Use the trigonometry values related to various standard angles like 0°, 30°, 45°, 60°, 90°, 180°, 270°, and 360° to make a tabular format. This trigonometry table is easy to use. It predicts the table values and uses the table to calculate trigonometric values of other remaining angles of a triangle.
The Trigonometric Values Table Is as Under:
| 𝚹 (°) |
0° |
30° |
45° |
60° |
90° |
180° |
270° |
360° |
|---|---|---|---|---|---|---|---|---|
| 𝚹(rad) |
0 |
π/6 |
π/4 |
π/3 |
π/2 |
π |
3π/2 |
2π |
| Sine |
0 |
1/2 |
1/√2 |
√3/2 |
1 |
0 |
-1 |
0 |
| Cosine |
1 |
√3/2 |
1/√2 |
1/2 |
0 |
-1 |
0 |
1 |
| Tan |
0 |
1/√3 |
1 |
√3 |
∞ |
0 |
∞ |
0 |
| Cot |
∞ |
√3 |
1 |
1/√3 |
0 |
∞ |
0 |
∞ |
| Cosec |
∞ |
2 |
√2 |
2/√3 |
1 |
∞ |
-1 |
∞ |
| Sec |
0 |
2/√3 |
√2 |
2 |
∞ |
-1 |
∞ |
-1 |
Let us learn Trigonometry Values of the triangle for different angles 0°, 30°, 45°, 60° and 90° concerning primary functions (Sine, Cosine, and Tangent) and secondary functions (Cosecant, Secant, and Cotangent).
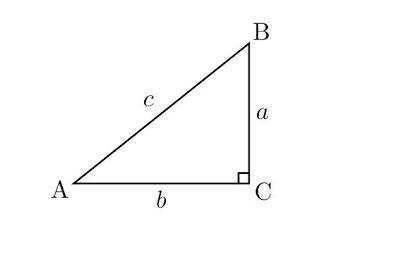
Suppose ABC is a right-angled triangle with ∠C = 90°, with AB as the hypotenuse, side AC adjacent to ∠A and side BC perpendicular to ∠C.
Now, the trigonometry values can be represented as under:
Primary Functions:
- sinθ = Side opp to θ / Hypo = CA/BA
- cosθ = Adj side to θ / Hypotenuse = BC/BA
- tanθ =Side opp to θ / Adj side to θ = CA/BC
Secondary Functions:
- Secθ = 1/Cosθ = Hypo/Adj side to angle θ = BA/ BC
- Cosecθ = 1/Sinθ = Hypo/Side opp to angle θ = BA/ CA
- Cotθ = 1/tanθ = Adj side to angle θ/Side opp to angle θ = BC/ CABC
From the above illustrations, we can derive the following:
- Secθ*Cosθ = 1
- Cosecθ*Sinθ = 1
- Cotθ*Tanθ = 1
Applicability of Trigonometry
Trigonometry is an important and scoring topic. The use of trigonometry is wide. Theoretically, the subject carries a weightage of 6 marks in 10th board exams.
Illustrated Examples
- Find the value of sin(90-45)°.
Ans: sin(90-45)° = cos 45° = 1/√2
- Suppose tan θ = 4 and sin θ = 6. Then find the value of cos θ?
Ans: We know, cos θ = sin θ/ tan θ
Therefore, cos θ = 6/4 = 3/2
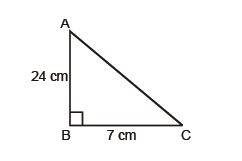
- In the below right-angled triangle ABC, AB = 24cm, BC = 7cm; Determine Sin A and Cos A
Ans: Let us calculate AC using the Pythagoras theorem,
AC2 = AB2 + BC2
AC2 = 625
AC = 25
Now, Sin A = BC/AC = 7/25
Cos A = AB/AC = 24/25
- Consider the above given question, Determine Sin C, Cos C
Ans: Sin C = AB/AC = 24/25
Cos C = BC/AC = 7/25
Frequently Asked Questions
Q: Who constructed the trigonometric values?
Q: Where can trigonometry concepts be used?
Q: What are the different functions of trigonometry?
- Sine function
- Cosine function
- Tan function
- Sec function
- Cot function
- Cosec function
Q: What are the formulas to state the six functions of trigonometry?
- Sine A = Opposite side/Hypotenuse
- Cos A = Adjacent side/Hypotenuse
- Tan A = Opposite side/Adjacent side
- Cot A = Adjacent side/Opposite side
- Sec A = Hypotenuse/Adjacent side
- Cosec A = Hypotenuse/Opposite side
Q: What is the meaning of trigonometry?
Maths Trigonometry Exam
Student Forum
Popular Courses After 12th
Exams accepted
CA FoundationExams accepted
ICSI ExamExams accepted
BHU UET | GLAET | GD Goenka TestBachelor of Business Administration & Bachelor of Law
Exams accepted
CLAT | LSAT India | AIBEExams accepted
IPMAT | NMIMS - NPAT | SET
Exams accepted
BHU UET | KUK Entrance Exam | JMI Entrance ExamBachelor of Design in Animation (BDes)
Exams accepted
UCEED | NIFT Entrance Exam | NID Entrance ExamBA LLB (Bachelor of Arts + Bachelor of Laws)
Exams accepted
CLAT | AILET | LSAT IndiaBachelor of Journalism & Mass Communication (BJMC)
Exams accepted
LUACMAT | SRMHCAT | GD Goenka Test