Trigonometry Graphs: Overview, Questions, Preparation

Sine, cosine, and digression are the three significant geometry proportions, in light of which capacities are characterized. The following are the diagrams of the three geometry capacities sin x, cos x, and tan x. In these geometry charts, x-hub estimations of the points are in radians, and on the y-pivot, its f(x) is taken, the estimation of the capacity at each given point.

y = sin x 

The roots or zeros of y = sin x is at the products of π 

The transgression diagram passes the x-pivot as wrongdoing x = 0 there. 

The time of the sine work is 2π. 

The tallness of the bend at each point is equivalent to the line estimation of sine. 

1 at π/2 -1 at (3π/2)

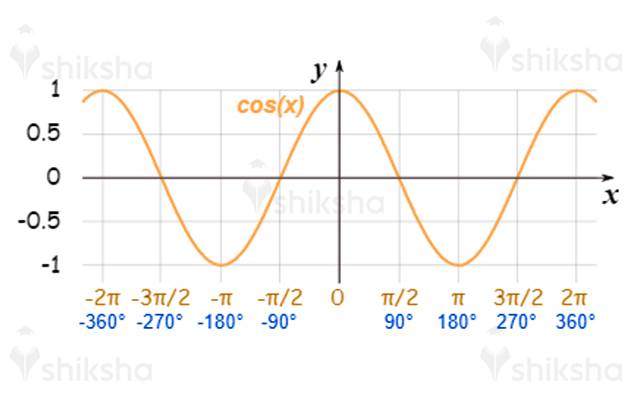
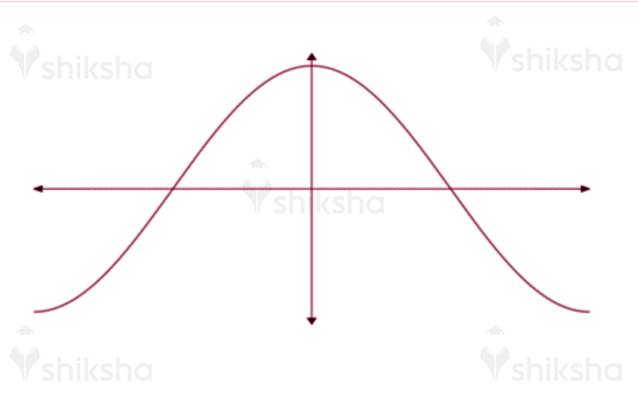
Cos Graph

y = cos x

sin (x + π/2 ) = cos x 

y = cos x chart is the diagram we get in the wake of moving y = sin x to π/2 units to one side 

The time of the cosine work is 2π. 

Max estimation of Graph Min estimation of the diagram 

1 at 0, 4π -1 at 2π

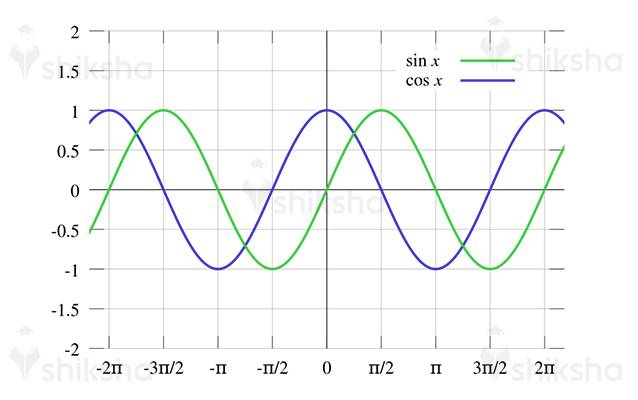
There are a couple of similarities between the sine and cosine charts, They are: 

• Both have a similar bend which is moved along the x-pivot 
• Both have adequacy of 1 
• Have a time of 360° or 2π radians 

The joined chart of sine and cosine capacity can be spoken to as follows.

The tank capacity is unique about sin and cos work. The capacity here goes among negative and positive boundlessness, getting through 0 over a π radian time. 

y = tan x 

The digression diagram has an indistinct abundance as the bend keeps an eye on the limitlessness. 

It likewise has a time of 180°, for example, π

Class 10: In the chapter Introduction of trigonometry, the graphs have been explained using the graph's elaboration and equations.

The chapter has a weightage of 12 Marks.

1. Which is meant by cos wave?

A cosine wave is a sign waveform with a shape indistinguishable from that of a sine wave, aside from each point on the cosine wave happening precisely 1/4 cycle sooner than the relating point on the sine wave.

2. What is a COS graph?

To chart the cosine work, we mark the point along with the level x pivot, and for each point, we put the cosine of that point on the vertical y-hub. The outcome, as seen above, is a smooth bend that differs from +1 to - 1. It is a similar shape as the cosine work yet dislodged to one side 90°

3. How can we know that the graph is of sin or cos?

In a cosine chart, a positive or negative number vertically flips the diagram and decides if the chart begins at the greatest (if it is specific) or least (if it is negative). A positive or negative number vertically flips the diagram for a sine chart as it does with a cosine diagram.

Q: What will be the graph for y = sin(x) for the region -360० ≤ x ≤ -360०

A:

 

Q: What will be the graph for y = cos(x) for the region -360० ≤ x ≤ -360०

A:

 

Q: What will be the graph for y = tan(x) for the region -360० ≤ x ≤ -360०

A:

 

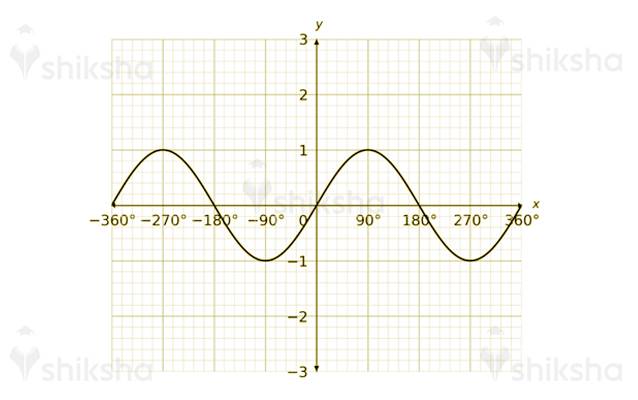
Q: The graph is for which form?

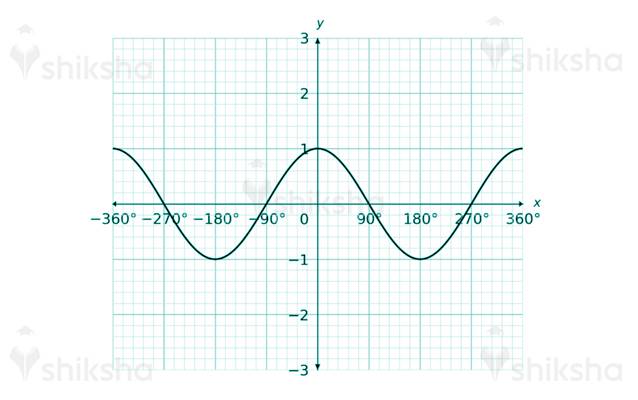
Q: The graph is for which form?