
- What is Modulus Function?
- Weightage of Modulus Function in Class 11
- Illustrated Examples of Modulus Function
- FAQs on Modulus Function
What is Modulus Function?
A modulus function is a function that takes an absolute value; for example, a number becomes greater or smaller. It defines the true extent of the sum of variables. The average is also regarded as an absolute value function. The product of this function will always equal a positive value, regardless of the data. It is seen as y=|x|. The plotting of such graphs is also a simple approach where the scope will be all values of input say x (all real numbers) and range will be all values of function (y = f(x) = all positive real numbers and 0).
Modulus Function Definition
A relation "f" is called a function if it maps each element of an initial segment of the universe to a single element in a series. The function f(x) of x is known as:
f(x) = |x|.
Or
y = |x|.
Where f: R→R and x belongs to R.
And |x| denotes the number mod x.
If x is positive, then only x will be produced by the function f(x). If x is negative, so the magnitude of x is what x is. Therefore, we should redefine the modulus function as follows:
Modulus Function Graph
Now, let us plot a graph for modulus function. Let x denote a variable whose values range from negative three to positive three, the domain of the graph. The graph should always be a continuous function of x at each value, as per the concept. Consider the table given where the y-axis shows the value of y and the x-axis shows the value of x; then we can plot the graph.
The graph indicates that the values of the modulus function remain positive for all the values of the variable, such as; x
When x = -3 then y = |-3| = 3
When x = -2 then y = |-2| = 2
When x = -1 then y = |-1| = 0
When x = 0 then y = |0| = 0
When x = 1 then y = |1| = 1
When x = 2 then y = |2| = 2
When x = 3 then y = |3| = 3
Weightage of Modulus Function in Class 11
This concept is taught under the chapter Relations and Functions. You will learn about the basics of this function and its uses. The weightage of this chapter is 6 marks in your final exam.
Illustrated Examples of Modulus Function
1. Solve modulus and find the interval of b for |b^2 – 5b + 6|
Solution:
|b^2 – 5b + 6| = |(b – 2)(b – 3)| = |f(b)|
As per modulus definition,
|f(b)| = f(b); if f(b) is positive
| f(b) |= -f(b); if f(b) is negative
f(b) = (b – 2)(b – 3) is positive or zero when b = (- ∞, 2] ∪ [3, ∞)
f(b) = (b – 2)(b – 3) is negative when b = (2, 3)
So, |b^2 – 5b + 6| = (b^2 – 5b + 6) when b = (-∞, 2] ∪ [3, ∞) and
|b^2 – 5b + 6| = -(b^2 – 5b + 6) when b = (2, 3)
2. Locate the domain and range of the feature below?
Y = |1−x|
Solution:
Y = |1 ‒ x|
Obviously, this is known as x x R. Then it's Domain R.
Right now |1 − x| ≥ 0 for all x ∈ R
So the range [0, ∞ )
3.Locate the domain and range of the feature below?
Y = 2 − |1 ‒ x|
Solution:
Y = 2 − |1 ‒ x|
Obviously, this is known as x x R. Then it's Domain R.
Right now |1 − x| ≥ 0 for all x ∈ R
or
−|1 − x| ≤ 0 ≤ 0
2 − |1 − x| ≤ 2 for all x'R's
Then the range is (−∞, 2]
FAQs on Modulus Function
Q: What does the modulus equation mean?
Q: What is the concept of modulus?
Q: What's the use of modulus in everyday life?
Q: What is the coding modulus?
Q: Is modulus function onto?
Maths Relations and Functions Exam
Student Forum
Answered 4 days ago
Yes, Class 12 Math Relations and Functions includes all the key topics as per requirements for CBSE Board Exams. Relations and Functions has several exercises with plenty of practice problems to help students understand the concepts better. We have designed solutions in a simple and clear manner to
P
Beginner-Level 2
Answered 4 days ago
Class 12 Math Relation and Function chapter have moderate weightage in the JEE Mains exam. Relation and function combined with sets comprises of 4-8 marks weight in the JEE Mains Exam. However, Students should know there is no fixed weightge of relation and fucntions chapter. Questions may be asked
E
Beginner-Level 2
Answered 4 days ago
Candidates must be aware of the important concepts discussed in the chapter and their application in other mathematics chapters. Students can check several fundamental and advanced topics discussed in the Relation and Function chapter.
- Basic Concepts: Definations, Sets cross product, Relation, Functi
P
Beginner-Level 2
Answered 4 days ago
Yes, Class 12 Math Relation and Function chapter is important for rither CBSE Board Exams or State Boards. The Relation and Function chapter have weightage of 6-8 marks in the CBSE board exam. Moreover Relation and function chapter forms the foundation for many other advanced topicssuch as types of
A
Beginner-Level 2
Popular Courses After 12th
Exams accepted
CA FoundationExams accepted
ICSI ExamExams accepted
BHU UET | GLAET | GD Goenka TestBachelor of Business Administration & Bachelor of Law
Exams accepted
CLAT | LSAT India | AIBEExams accepted
IPMAT | NMIMS - NPAT | SET
Exams accepted
BHU UET | KUK Entrance Exam | JMI Entrance ExamBachelor of Design in Animation (BDes)
Exams accepted
UCEED | NIFT Entrance Exam | NID Entrance ExamBA LLB (Bachelor of Arts + Bachelor of Laws)
Exams accepted
CLAT | AILET | LSAT IndiaBachelor of Journalism & Mass Communication (BJMC)
Exams accepted
LUACMAT | SRMHCAT | GD Goenka Test

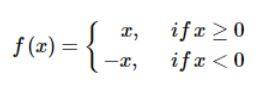

Will Class 12 Math Relation and Function NCERT Solutions be enough to prepare for the CBSE Boards exams?