- Trigonometric Equations
- Trigonometric Equation Formulas
- Trigonometric Identities
- Trigonometric Equations and their Solutions
- Trigonometric Ratios in Case of Complementary Angles
- About the Topic in Class X and XII
- Illustrated Examples
- Frequently Asked Questions
Trigonometric Equations
The trigonometric equation is an important topic. The topic basically involves the equations of more than one trigonometric ratios having unknown angles. It is demonstrated as the ratios of sin, cos, tan, cot, sec, and cosec angles. And the values that satisfy the trigonometric equations are known as the solutions of the respective trigonometric equations.
Trigonometric Equation Formulas
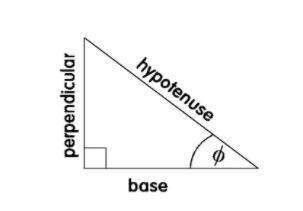
- sin X = PerpendicularHypotenuse
- cos X = BaseHypotenuse
- tan X = PerpendicularBase
- cot X = BasePerpendicular
- sec X = HypotenuseBase
- cosec X = HypotenusePerpendicular
Some values of standard angles in trigonometry are -
Trigonometric Identities
Since the right angle triangle, XYZ follows the property of Pythagoras theorem; therefore the three trigonometric equations we get are:
- sin2x + cos2x = 1
- cosec2x – cot2x = 1
- sec2x – tan2x = 1
Trigonometric Equations and their Solutions
Those equations which involve variables in trigonometric functions are called Trigonometric Equations.
When the value of variable x ranges from 0≤x≤2π in solution, such solutions are principal solutions, whereas, if there is an integer "n" in the solution, it is a general solution.
| Equations |
General Solutions |
|---|---|
| sin A = 0 |
A = nπ |
| cos A = 0 |
A = (π/2 + nπ) |
| cos A = 0 |
A = nπ |
| sin A = 1 |
A = (2nπ + π/2) = (1+4n) π/2 |
| cos A = 1 |
A = 2nπ |
| sin A = sin α |
A = nπ + (-1)n α, α ∈ [-π/2, π/2] |
| cos A = cos α |
A = 2nπ ± α, α ∈ (0, π] |
| tan A = tan α |
A = nπ + α, α ∈ (-π/2, π/2] |
| sin 2A = sin 2α |
A = nπ ± α |
| cos 2A = cos 2α |
A = nπ ± α |
| tan 2A = tan 2α |
A = nπ ± α |
Trigonometric Ratios in Case of Complementary Angles
- cos X = sin (90 – X)
- sin X = cos (90 – X)
- cot X = tan (90 – X)
- tan X = cot (90– X)
- cosec X = sec (90 – X)
- sec X = cosec (90– X)
About the Topic in Class X and XII
Trigonometry is a vital section of mathematics. The chapter is present in class X and class XI; trigonometry applications are also present in class XII. In class X, the weightage of this chapter is nearly 12 marks, and around 5 to 6 questions are asked every year from this chapter. The question ranges from moderate to tough level in case of difficulty.
Trigonometry is a part of many topics like calculus, integration, conic section, sets and functions. In class X, the chapter contents of the Introduction to Trigonometry are:
- Trigonometric Ratios and Identities
- Specific and Complementary Angles' Trigonometric Ratios
Illustrated Examples
1. What will be the principal solutions of tan x = – 1/(√3)?
We know, tan(π/6) = 1/(√3)
So, -tan(π/6) = – 1/(√3)
= tan (π – π/6 )
Further, -tan(π/6) = tan (2π – π/6)
= – 1/(√3)
Therefore the principal solutions will be tan (5π/6) and tan (11π/6).
2. Estimate cosec A = 2?
Since cosec A = cosec π/6 = 2,
A = (-1)n π/6 + nπ.
3. Express the trigonometric equation cos 75° + cot 85° in between angles from 0° and 45°.
cos 75° + cot 85° = cos (90° – 15°) + cot (90° – 5°)
= sin 15° + tan 5°.
Frequently Asked Questions
Q: Does sin 15 have any value? If yes, what is it?
Q: How to convert a degree into radian?
Q: How many radians are present in 180°?
Q: What is the range of f(A) = sin A?
Q: What does sin 2A equal?
Maths Trigonometry Exam
Student Forum
Popular Courses After 12th
Exams accepted
CA FoundationExams accepted
ICSI ExamExams accepted
BHU UET | GLAET | GD Goenka TestBachelor of Business Administration & Bachelor of Law
Exams accepted
CLAT | LSAT India | AIBEExams accepted
IPMAT | NMIMS - NPAT | SET
Exams accepted
BHU UET | KUK Entrance Exam | JMI Entrance ExamBachelor of Design in Animation (BDes)
Exams accepted
UCEED | NIFT Entrance Exam | NID Entrance ExamBA LLB (Bachelor of Arts + Bachelor of Laws)
Exams accepted
CLAT | AILET | LSAT IndiaBachelor of Journalism & Mass Communication (BJMC)
Exams accepted
LUACMAT | SRMHCAT | GD Goenka Test