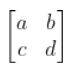Matrices and Determinants: Overview, Questions, Preparation

An orderly arrangement of numbers or functions in a rectangular form is defined as a matrix. A matrix is denoted by capital letters. The numbers or functions are called elements and are distinguished by its position in rows and columns. The elements are represented by a_ij, where ‘i’ denotes the corresponding row, and ‘j’ denotes the corresponding column.

Let A be a matrix, A=

 

In the above example above, a₁₁=1, a₁₂= 2, a₁₃=3,a₂₁=4 and so on. 

Order of the matrix is denoted as m n, where m is the number of rows and n is the number of columns a matrix has. The number of rows multiplied by the number of columns gives the number of elements, i.e., number of elements=m x n. In the above example above, an order of the matrix = 3x3 and nNumber of elements=3x3=9.

Properties ( when A and B are two matrices)

• AB ≠ BA
• (AB)C = A(BC)
• A.(B+C) = A.B + A.C

Determinants

For every square matrix, a number can be computed (real/complex), called the particular matrix’s determinant.

For instance, consider a matrix of order 2, A=

[A]

Then determinant A, denoted by:

= ad - bc

For a matrix of order 3, a determinant can be calculated by expanding a determinant along a row or column. Hence, there are six ways to compute a determinant of order 3, along the three rows or [A] along with the three columns. Let us understand it better using an example.

Properties

• The values of a determinant remain unchanged even after interchanging its rows and columns.
  
• The sign of a determinant changes if any two rows or columns are interchanged.
  
• The value of a determinant in which any two rows are identical is zero.
  
• If each element of a row or column is multiplied by a constant, then the value gets multiplied by the same constant.
  
• If some or all elements of a row or column are expressed as the sum of two or more items, then the determinant can be defined as the sum of two or more determinants.
  
• If equimultiples of corresponding elements are added to each element of a row or column, then the determinant’s value remains the same.
  

The fundamentals of matrix and determinants are introduced to students in grade 12. The CBSE Board gives a weightage of 12 marks for the full unit of Algebra, under which these topics are discussed. 

1. In the matrix A= 

Solution:

The order of the matrix

The elements a₁₃, a₂₁,  a₃₃, a₂₄, a₂₃

The number of rows is 3, and the number of columns is 4. Order= 34.
a₁₃=19,
a₂₁=35,
a₃₃= - 5,
a₂₄=12,
a₂₃= 5/2.

2. Evaluate the determinant 

Solution:

= 2x(-1) - (-5) x 4
 = - 2 + 20= 18. 

3. Evaluate the determinant 

Solution:

= (cosθ x cosθ) - (sinθ x - sinθ)

= cos²θ + sin²θ

=1

Q: What are Name the different types of matrices?.

Q: When are two matrices equal?

Q: Does every matrix have its corresponding determinant?

Q: What is a determinant of the matrix of order 1?

Q: What is the determinant’s value if all the row or column elements are zeroes?

• Column matrix
• Row matrix
• Square matrix
• Diagonal matrix
• Scalar matrix
• Identity matrix
• Zero matrix