Adjacency Matrix: Overview, Questions, Preparation

Matrices are an important tool in mathematics. It helps in simplifying big data. 

What is a Graph?

A graph is a mathematical structure used to display relationships between objects. It is made up of nodes, which are connected by edges. 

Adjacency matrix means a square matrix which is used to represent a finite graph. With this kind of matrix, we can find out whether or not the vertices are adjacent on the graph. 

The adjacency matrix for a graph with n vertices is a n*n matrix.

Undirected Graphs

Undirected graphs are bidirectional in nature; that is, their edges can be directed in two ways.

Directed Graphs

Directed graphs have only one direction, that is, their edges can be directed in one and only one way.

Properties of Adjacency Matrices

Some of the properties of matrix related to the graph:

Spectrum

The adjacency matrix is symmetric for an undirected graph. A symmetric matrix is equal to its transpose matrix. Thus, it has a set of real eigenvalues and an orthogonal eigenvector basis. This set of eigenvalues of the graph is known as its spectrum.

Isomorphisms

Isomorphism means similarity. When two graphs are similar in nature, and if one graph can be obtained using the other given graph, they are known as isomorphic.

Matrix powers

Powers are beneficial in matrices. They give you a lot of information regarding matrices. You can use the matrix’s power to gain knowledge about a graph’s path.

Creating an Adjacency Matrix:

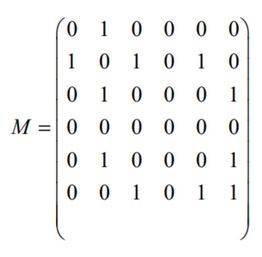
Look at the graph given below:

Taking A as vertex 1, B as vertex 2, etc., the adjacency matrix for this graph is

Source: NCERT

This chapter is a part of Class 12th maths and carries 10 marks. In this chapter, you will learn about various types of matrices and graphs with matrices.

Solution.

This is a |𝑉| × |𝑉| matrix. (𝑀𝑀^T)_ii is the degree of 𝑣_i. (𝑀𝑀^T)_ij for 𝑖 ≠ 𝑗 is the number of edges between 𝑣_i.and 𝑣_j. Let 𝐷 be a diagonal matrix with 𝐷ii being the degree of 𝑣_i We have, 𝑀𝑀^T = 𝐴 + 𝐷.

2. In a connected graph, what is the distance between two vertices 𝑣_i and 𝑣_j. if k is the smallest integer for which [X^k]_ij not equal to 0?

Solution.

Given that k is the smallest integer such that [X^k]_ij not equal to 0. Therefore, there are no edge sequences of length 1, 2, ..., k −1 and no paths of length 1, 2, or k−1 between vertices 𝑣_i. and 𝑣_j. Thus the shortest path between 𝑣_i.and 𝑣_j.is of length k so that d(𝑣_i., 𝑣_j. ) = k.

3. Prove τ(K_n) = n^n-2.

Solution.

Here, Q = H −X = (n−1)I −(J −I) = nI −J 

The cofactor of q₁₁ is the (n−1)×(n−1) determinant given by

Subtracting the first row from each of the others and then adding the last n−2 columns to the first,

Expanding with the help of the first column, we have a cofactor of q₁₁ = n^n-2 ,Thus,τ(K_n) = n^n-2

Q: What are the areas in which matrices can be applied?

Q: What is a matrix function?

Q: What is the number of two-step sequences between vertex i and vertex j in a graph with adjacency matrix M?

Q: What is the sum of the elements of row i of the adjacency matrix of a graph?

Q: What is the sum of the elements of column i of the adjacency matrix of a graph?