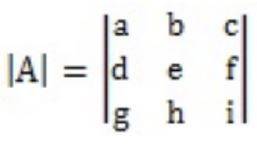Determinant of a 3 x 3 Matrix: Overview, Questions, Preparation

Matrices are a square or rectangular arrangement of different numbers or variables in rows and columns. The determinant of a matrix was developed to solve the linear equations easily. Always remember, a determinant can only be found out if it is a square matrix. A determinant is represented as |A| or det |A|.

3 x 3 matrix.

Determinant of a 3 x 3 matrix

There are two ways to determine the determinant of a 3 x 3 matrix. A 3 x 3 matrix means there are 3 rows and 3 columns in the matrix.

1. General Method - This method is widely followed where a 3 x 3 matrix is broken down into two 2 x 2 determinant matrices, which would help us find the determinant of a 3 x 3 matrix.

2. Shortcut method- This is an intelligent method where the determinants of a 3 x 3 matrix are calculated by multiplying and adding (subtracting) all the elements in their adjoining module without expanding like the general method. 

The determinant is used to solve various kinds of calculations and see its uses in calculus, linear algebraic equations, and advanced geometry. 

Importance of a Determinant 

The determinant helps in solving the linear equation by providing unique circumstances in which we get an outcome or a result of the given linear equation. It also helps to find the inverse of a matrix. 

The chapter ‘Matrices’ talks about Matrices, their types, and the various types of equations. The chapter talks about different operations, the transpose of a matrix, symmetric and skew-symmetric matrices, elementary operation of a matrix, and invertible matrices.

Illustrative Examples on Determinants of Matrix

1. If A, B are symmetric matrices of the same order, then AB - BA is 

1. Skew symmetric matrix
2. Zero matrix
3. Symmetric matrix
4. Identity matrix

Solution.

Ans- (a)

b + 4d = 2            2b + 5d = 4        3b + 6d = 6

= a + 4c = -7
= a = -7 - 4c

So, 2a + 5c = -8
= 2*(-7 - 4c) + 5c = -8
= c = -2
= a = 1

Now using the same process for the other two unknowns. 
= b + 4d = 2
= b = 2 - 4d

So, 2b + 5d = 4
= 2*(2-4d) + 5d = 4
= d = 0
= b =2

So matrix X = 

3. If the matrix A is both symmetric and skew-symmetric, then 

1. A is a square matrix
2. A is a zero matrix
3. A is a diagonal matrix
4. None of these

Solution.

If matrix A is symmetric  A^T =A
If matrix A is skew-symmetric A^-T =A

Also, the diagonal elements are zero.
A = A^T = - A

This is only possible when matrix A is a zero matrix.

So, matrix A is a zero matrix.

4. If A is a square matrix, such that A² =A, then (I + A)³ - 7A is equal to

1. A
2. I
3. 3A
4. I - A

Solution.

Given A² =A

= (I + A)³ - 7A = I³ + A³ + 3I²A + 3IA² - 7A

= I + A² +3A + 3A - 7A

= I + 7A - 7A

= (I + A)³- 7A = I

So, the  answer is (b).

Q: What is a matrix?

Q: What is a square and rectangle matrix?

Q: What is a determinant?

Q: What is the importance of a determinant?

Q: How is the determinant of a 3 x 3 matrix found?