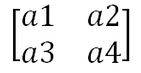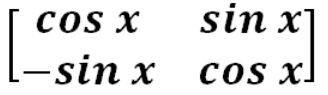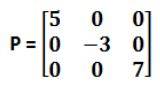Orthogonal Matrix: Overview, Questions, Preparation

In mathematics, we all know that a matrix is an arrangement of numbers in rows and columns in a rectangular array. When a square matrix(matrix whose rows and columns are equal in number)whose inverse and transpose are identical, then the square matrix is orthogonal. Suppose we have a square matrix X of n*n order and if X^T(Transpose) = X^-1(Inverse), then X will be an orthogonal matrix.

The determinant of Orthogonal Matrix

Let A be a 2x2 square matrix, A =

Therefore whenever we evaluate the determinant of A,
|A| = a1.a4 - a2.a3, then |A| will always result into ±1 if it is a square matrix.

Orthogonal Matrix Properties

• Only from the square matrix, we can obtain an orthogonal matrix.
• All the elements present in the orthogonal matrix are real elements.
• All the Identity matrices are the perfect example of an orthogonal matrix.
• The determinant of an orthogonal matrix(denoted by O) is either +1 or -1.
• If a matrix X is orthogonal, then its transpose, as well as its inverse matrix, will also result in an orthogonal matrix.

An orthogonal matrix is a part of class XII mathematics' chapter Matrices; the respective chapter is highly crucial for class XII and other competitive exams. In class XII mathematics exam, the chapter's question holds a total weightage by 8 to 10 marks. 

The chapter of matrices in class XII mathematics also contains other topics like

• Diagonal Matrix: In this matrix, all the non-diagonal elements are zero.
• Square Matrix: When the number of columns and rows are equal.
• Scalar Matrix: When all the diagonal elements in a diagonal matrix are identical.
• Identity Matrix: When all the diagonal elements are 1, the rest are 0 in a zero matrix.

Apart from that, the chapter also includes -

• operations on the matrices
• finding determinants
• finding the matrix's transpose and inverse
• calculating minors and co-factors, etc.

1.Check whether the matrix X is an orthogonal matrix or not?
X=

Solution.

We know that the orthogonal matrix's determinant is always ±1.
The determinant of X = cos x.cos x - sin x.(-sin x) 
= cos²x + sin²x = 1.
Value of |X| = 1, Hence it is an orthogonal matrix.

2. We have a matrix P of order 3 x 3.  Check if P is an orthogonal matrix or not?

Solution.

We can see that P is a diagonal matrix, and if we calculate the determinant of P and its transpose, then it will be equal. And this satisfies the property of the orthogonal matrix. Hence P is an orthogonal matrix.

3. Prove orthogonal property that multiplies the matrix by transposing results into an identity matrix if A is the given matrix.  

Solution.

Q:  What do we receive from the square matrix multiplication and transpose when the square matrix is orthogonal?

Q: Does the product of 2 orthogonal matrices also result in an orthogonal matrix?

Q: What is the Orthogonal Group?

Q: What is the determinant of identity and a zero matrix?

Q: What is the Diagonal Matrix?