Equation of Motion
The equation of motion determines the behavioural pattern of the physical system of the motion. It is part of a function of the equation of motion.
Broadly, there are three equations of motion, focusing on velocity, displacement, and acceleration.
Equations of motion:
- First equation – v = u + at
- Second equation – s = u + ½ at2
- Third equation – v2 = u2 + 2as
Derivation of Equations of Motion
The equation of motion can be derived using three methods,
- Simple algebraic method
- Graphical method
- Calculus method
Derivation of Equations of Motion by the Calculus Method
The equation of motion by calculus method can be determined, and velocity and acceleration can be identified. It is important for the understanding of physical quantities in motion.
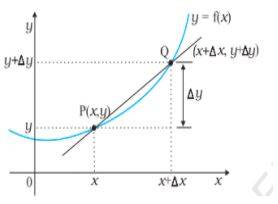
Let us make an equation using a quantity (y) and a single variable (x). it can be written as:
y = f (x)
let’s take a step further and see the diagrammatic representation:
Image source - ncert
P and Q are joined by a slope, and the equation of slope is:
This is the equation by differential calculus.
- Derivation of the first equation
The rate of change of velocity is acceleration,
a = dv / dt
it can also be written as:
adt = dv
after integrating both the equations we get:
∫t0adt=∫vudv
at = v-u
after rearranging we get,
| V = u + at |
First equation of motion by calculus methods.
- Derivation of the second equation
The change rate of displacement is velocity.
It can be equated as:
v = ds/dt
After rearranging we get,
ds = vdt
let’s integrate both the equations together,
ds = (u +at) dt
ds = (u +at) dt=(udt + atdt)
after simplifying it further, we get:
| = ut + ½ at2 |
- Derivation of the third equation
As we discussed earlier that the rate of change in velocity is called acceleration, and it is represented as follows:
a = dv/dt
as discussed in the second equation that the rate of change in displacement is velocity and is written as,
v = ds/dt
by multiplying both the above-written equation, we get,
a ds/dt = v dv/dt.
It can be rewritten as
| V2 = u2 +2as |
Weightage in Class 11
The chapter ‘Introduction to Motion’ holds a weightage of 5 marks in total. It consists of one short question of 2 marks and another short type question consisting of 3 marks.
Illustrated Examples
1. Explain the derived equation for the second equation of motion.
Derived equation for the second equation of motion is - V = ut + ½ at2
2. Explain the formula used in defining the third equation of motion.
Formula for the third equation of motion is – v2 = u2 + 2as
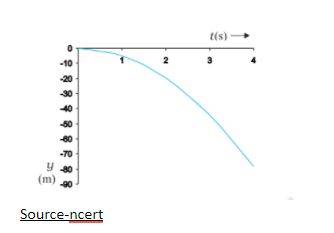
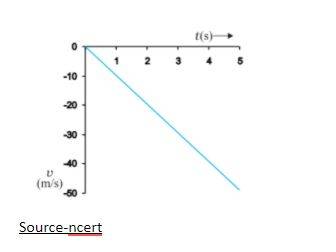
3. Provide an illustrated example of an object in a free-fall motion in which there is a variation of distance concerning time.
FAQs on Derive Equation of Motion by Calculus Method
Q: What’s the formula for the second equation of motion?
Q: What’s the derived equation of the first equation of motion?
Q: What are different methods that are used to derive motion equations?
- Simple algebraic method
- Graphical method
- Calculus method
Q: What are the main factors every equation of motion focuses on?
Q: Provide an example of motion in a free fall where velocity is variant.
News & Updates
Motion Exam
Student Forum
Answered a month ago
Ecole Intuit Lab Bengaluru BDes (Hons) in Animation and Motion Design is a 4 year UG programme. The Institute offers this programme in full-time mode, on the basis of merit. Therefore, the eligibility criteria includes a qualification of Class 12 with a minimum of 45% aggregate. Intuit Lab Bengaluru
A
Beginner-Level 4
Popular Courses After 12th
Exams: BHU UET | KUK Entrance Exam | JMI Entrance Exam
Bachelor of Design in Animation (BDes)
Exams: UCEED | NIFT Entrance Exam | NID Entrance Exam
BA LLB (Bachelor of Arts + Bachelor of Laws)
Exams: CLAT | AILET | LSAT India
Bachelor of Journalism & Mass Communication (BJMC)
Exams: LUACMAT | SRMHCAT | GD Goenka Test
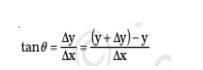
What is the fee for BDes (Hons) Animation & Motion Design at Ecole Intuit Lab Bengaluru?