Period of a Function: Overview, Questions, Preparation

The period of a function is an important concept for trigonometry. It is used to study the repetition pattern of a function like a sine or a cosine, etc. The period of a function also represents the repetition cycle on the graph.

In this write-up, we will understand and learn about the concept of a period of a function, the steps to find a period of function for different scenarios, and some examples of it.

The time interval between two waves of a function is called the period of a function. However, any function that repeats its value at a regular and definite period or intervals can be termed a Periodic Function.  

Let us understand with the help of an example. Suppose we have a function ‘p’ that would repeat itself at a period ‘n’. Then the equation will be:

p(a+n)’ = p(a) for every value of n>0.

It shows that the after ‘n’ period function ‘p’ will repeat itself.

1. When a function repeats its value at a constant period, it is termed a periodic function.
2. It can be represented like p(y) = p(y+q), q is any real number and the period of the represented function.
3. The period can be defined as the time interval between the two repetitions of the waves.

When the trigonometric functions are plotted on the graph, the trigonometric functions' constant repeating of the waves will be produced. The waves have a high point, i.e. peaks and a low point, i.e. troughs.

However, the whole length of one complete cycle is known as the Period of a trigonometric function. Generally, there are three basic trigonometric functions, i.e. cos, sin, and tan having periods 2π, -2π, and π, respectively.

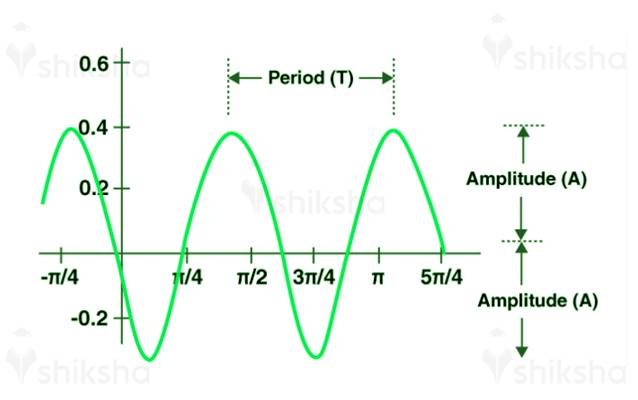
In the above image,

Period: ‘T’ will be representing the distance between two repeating points of the function, which is termed as Period.

Amplitude: Amplitude is represented by ‘A.’ It can be defined as the distance between the midpoint of the lowest or highest point of the function on the graph.

Moreover, the above image representing the sine and cosine functions period forms on the graph. We can write it as:

Sin (aϴ) = 2πa and cos (aϴ) = 2πa  

1. Figure out the frequency and period for the equation y = 4 sin(6x – π) + 2.

Solution: 

The given equation is of the form q=A⋅sin(fp−h)+k 

Here A indicates the amplitude, f indicates the frequency, h represents the horizontal shift, followed by k that represents the vertical shift.

By analysing the equation, we can evaluate the frequency f = 6.

Therefore, the period is 2π/f and resulted as 2π/6=π/3.

2. Measure the period of Sin2a.

Solution: 

By following the

trigonometric identity,

⇒sin2a =1+cos2a/2                                                         

⇒sin2x=1+cos2x2

Now, compare the above with af (bx+c) + daf (bx+c) +d, then the magnitude of “b” i.e. |b| will be 2. Therefore, the period of cosine will be 2π. It means the period of sin2a :

⇒T=2π/2=π

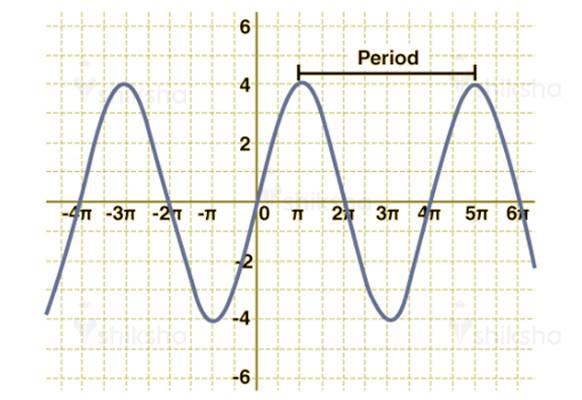
3. Represent Graph of y= 4 sin(m/2)

Solution:

Period = 4π

Amplitude = 4

Minimum and Maximum value is -4 and 4, respectively.

Range = [-4.4]

Axis y = 0 [x-axis]

Domain: {x: x∈ R}

FAQs

Q: What is Frequency?

Q: Define the fundamental period of a function?

Q: Mention the formula for calculating the period of a function?

Q: Calculate period of a function q(y) = 9Sin(6qy7+5)

Q: Does constant function periodic?