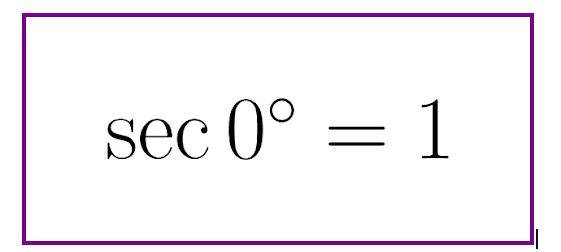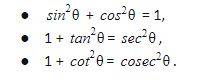This chapter has multiple topics listed below:
Trigonometric FunctionsTrigonometry TableTrigonometry FormulasTrigonometric IdentitiesTrigonometric RatiosTrigonometry ValuesTrigonometric EquationsAngle of ElevationApplications of TrigonometryTan 60 degreesTan 90 degreesAngle of DepressionCos MeaningHyperbolic FunctionsLaw of CosinesSec 30Sec 0Sec 60Sin 1Sin 45 degreesPeriod of a FunctionSin Cos Tan ValuesTrigonometry AnglesTrigonometry GraphsDegrees to Radians
Table of content
- Sec 0
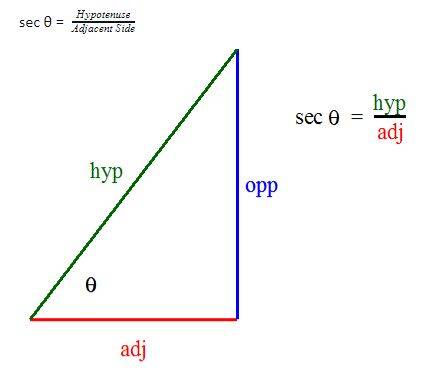
- In trigonometry, sec (also known as secant) of an angle is hypotenuse divided by the length of the adjacent side.
- Suppose ABC is a right-angled triangle where the side of B is right-angled, then,
- Finding the Value of Sec 0
- Angle 0 lies in the first quadrant between 0 to 90 degrees. And the value of sin, cos, and tan in the first quadrant is always positive. Hence the value of sec will also be positive. Therefore the sec 0 value will be:
- 1/cos θ=sec θ, (θ = 0)
- 1/cos θ=sec 0,
- value of cos 0 is 1, therefore sec 0 = 1.
- Other Angles
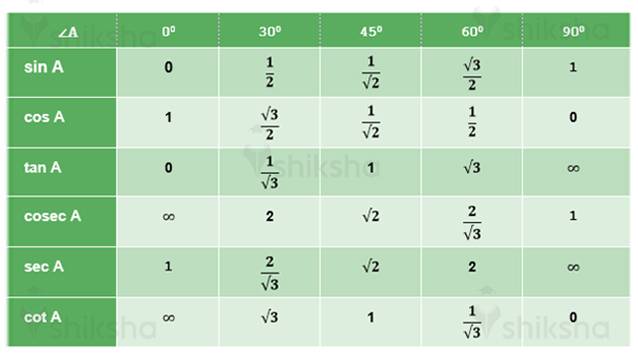
- Apart from sec or secant, there are also other angles that are covered in the chapter, and they are sin, cos, tan, cot, cosec. For a right-angled triangle ABC with an angle θ,
- sin θ = P/H
- cos θ = B/H
- tan θ = sin θ /cos θ = P/B
- sec θ = 1/cos θ = H/B
- cosec θ = 1/sin θ = H/P
- cot θ = 1/tan θ = B/P
- here B = Base, P = Perpendicular, H = Hypotenuse.
- Chapter Weightage
- The chapter is crucial in class X and further classes. Chapters on Trigonometry and its applications are also present in class XI and class XII. It holds a weightage of around 10 to 12 marks. Every year around 5 to 6 questions are asked from the chapter in class X exams.
- Illustrative Examples
- We can write the above expression as tan65°/cot25°,
- we know that tan θ can also be written as a cot(90° - θ)
- therefore, tan 65° = cot 25°
- hence, cot25°/cot25° = 1.
- We know that sin 30 ° = 1/2 and sec 60° = 2
- Therefore, A-B = 30° and A+B=60°
- On solving A and B, we will get, A = 45° and B = 15°.
- Applying Pythagoras Theorem,
- OQ2 = OP2+ PQ2
- (1 +PQ2) = OP2 +OQ2,(given OQ-PQ =1)
- 1+2PQ = OQ2
- 1+2PQ = 72
- Therefore we will get PQ = 24cm and OQ = 25cm,
- Hence cos Q = 24/25 and sin Q = 7/25.
- Frequently Asked Questions
- Ans. 1/sec θ = cos θ.
- Ans. 1 + tan2θ= sec2θ.
- Ans. The value of sec 90 is infinite or not defined.
- Ans. The value of sin(A+B) = sin A.cos B + cos A.sin B.
- Ans. The range of sec θ is ( -∞, -1 ] U [ 1, ∞ ).
View More
Sec 0
In trigonometry, sec (also known as secant) of an angle is hypotenuse divided by the length of the adjacent side.
Suppose ABC is a right-angled triangle where the side of B is right-angled, then,
Finding the Value of Sec 0
Angle 0 lies in the first quadrant between 0 to 90 degrees. And the value of sin, cos, and tan in the first quadrant is always positive. Hence the value of sec will also be positive. Therefore the sec 0 value will be:
1/cos θ=sec θ, (θ = 0)
1/cos θ=sec 0,
value of cos 0 is 1, therefore sec 0 = 1.
Other Angles
Apart from sec or secant, there are also other angles that are covered in the chapter, and they are sin, cos, tan, cot, cosec. For a right-angled triangle ABC with an angle θ,
sin θ = P/H
cos θ = B/H
tan θ = sin θ /cos θ = P/B
sec θ = 1/cos θ = H/B
cosec θ = 1/sin θ = H/P
cot θ = 1/tan θ = B/P
here B = Base, P = Perpendicular, H = Hypotenuse.
Chapter Weightage
The chapter is crucial in class X and further classes. Chapters on Trigonometry and its applications are also present in class XI and class XII. It holds a weightage of around 10 to 12 marks. Every year around 5 to 6 questions are asked from the chapter in class X exams.
Illustrative Examples
We can write the above expression as tan65°/cot25°,
we know that tan θ can also be written as a cot(90° - θ)
therefore, tan 65° = cot 25°
hence, cot25°/cot25° = 1.
We know that sin 30 ° = 1/2 and sec 60° = 2
Therefore, A-B = 30° and A+B=60°
On solving A and B, we will get, A = 45° and B = 15°.
Applying Pythagoras Theorem,
OQ2 = OP2+ PQ2
(1 +PQ2) = OP2 +OQ2,(given OQ-PQ =1)
1+2PQ = OQ2
1+2PQ = 72
Therefore we will get PQ = 24cm and OQ = 25cm,
Hence cos Q = 24/25 and sin Q = 7/25.
Frequently Asked Questions
Ans. 1/sec θ = cos θ.
Ans. 1 + tan2θ= sec2θ.
Ans. The value of sec 90 is infinite or not defined.
Ans. The value of sin(A+B) = sin A.cos B + cos A.sin B.
Ans. The range of sec θ is ( -∞, -1 ] U [ 1, ∞ ).
Maths Trigonometry Exam
Student Forum
Popular Courses After 12th
Exams accepted
CA FoundationExams accepted
ICSI ExamExams accepted
BHU UET | GLAET | GD Goenka TestBachelor of Business Administration & Bachelor of Law
Exams accepted
CLAT | LSAT India | AIBEExams accepted
IPMAT | NMIMS - NPAT | SET
Exams accepted
BHU UET | KUK Entrance Exam | JMI Entrance ExamBachelor of Design in Animation (BDes)
Exams accepted
UCEED | NIFT Entrance Exam | NID Entrance ExamBA LLB (Bachelor of Arts + Bachelor of Laws)
Exams accepted
CLAT | AILET | LSAT IndiaBachelor of Journalism & Mass Communication (BJMC)
Exams accepted
LUACMAT | SRMHCAT | GD Goenka Test
News & Updates
Latest NewsPopular News