Combination of Resistors - Series and Parallel is an important topic from Current Electricity. In electrical circuits, resistors are components used to impede the flow of electric current. When designing circuits or solving problems related to resistors, it's essential to understand how resistors can be combined in series and parallel configurations. Let's explore both series and parallel combinations of resistors. The NCERT Class 12 Phyics Solutions on Combination of Resistors - Series and Parallel are given below.
Series Combination
In a series combination of resistors, they are connected end-to-end, forming a single path for the current to flow through. The total resistance in a series circuit is the sum of the individual resistances. Mathematically, if you have 'n' resistors (R1, R2, R3, ..., Rn) connected in series, the total resistance (Rtotal) can be calculated as:
Rtotal = R1+ R2+ R3 ... Rn
The current remains the same throughout a series circuit, as it has only one path to follow. Voltage, on the other hand, is divided across the resistors, and it is proportional to the resistance of each resistor. Ohm's Law can be used to calculate the voltage drop across each resistor:
V1 = I.R1
V2 = I.R2
V3 = I.R3
Parallel Combination
In a parallel combination of resistors, each resistor is connected across the same two points, creating multiple paths for the current to flow. The total resistance in a parallel circuit is different from the series case. To calculate the total resistance (Rtotal) of 'n' resistors (R1, R2, R3, ..., Rn) connected in parallel, you use the following formula:
(1/Rtotal) = (1/R1 + 1/R2 + 1/R3 ... Rn)
In a parallel circuit, the voltage across each resistor is the same, as they are all connected across the same points. However, the current is divided among the resistors, and the amount of current through each resistor is inversely proportional to its resistance. Ohm's Law can be used to calculate the current through each resistor:
I1 = V/R1
I2 = V/R2
I3 = V/R3
Series Resistors and Parallel Resistors: Applications
Series Resistors: Series combinations are often used when you want to add resistance to a circuit or when you have multiple devices that require the same current. For example, Christmas lights are connected in series.
Parallel Resistors: Parallel combinations are used when you want to divide the current among different branches of a circuit or when you have devices that require the same voltage. Household appliances are typically connected in parallel.
Understanding how to combine resistors in series and parallel is crucial in circuit design and troubleshooting, as it allows you to control current and voltage in electronic devices and ensure they function as intended.
FAQs on Combination of Resistors - Series and Parallel
Q. A battery of emf 10 V and internal resistance 3 Ω is connected to a resistor. If the current in the circuit is 0.5 A, what is the resistance of the resistor? What is the terminal voltage of the battery when the circuit is closed?
A EMF of the battery = 10 V
Internal resistance of the battery, r = 3 Ω
Current in the circuit, I = 0.5 A
Let the resistance of the resistor be R
According to Ohm’s law
I = E/ (R+r)
R + r = E/I or R = E/I - r = 10/0.5 - 3 = 17 Ω
Terminal voltage of the battery when the circuit is closed is given by
V = IR = 0.5 X 17 = 8.5 V
Therefore the resistance is 17 Ω and the terminal voltage is 8.5 V
Q. (a) Three resistors 1 Ω, 2 Ω, and 3 Ω are combined in series. What is the total resistance of the combination? (b) If the combination is connected to a battery of emf 12 V and negligible internal resistance, obtain the potential drop across each resistor.
A.
- The equivalent resistance of the resistor in series is given by
- R = 1 + 2 + 3 = 6 Ω
- From Ohm’s law, I = V/R we get I = 12/6 = 2 A.
- Potential drop across 1 Ω resistor = I X R = 2 X 1 = 2 V
- Potential drop across 2 Ω resistor = I X R = 2 X 2 = 4 V
- Potential drop across 3 Ω resistor = I X R = 2 X 3 = 6 V
Q (a) Three resistors 2 Ω, 4 Ω and 5 Ω are combined in parallel. What is the total resistance of the combination? (b) If the combination is connected to a battery of emf 20 V and negligible internal resistance, determine the current through each resistor, and the total current drawn from the battery.
A. (a)
- Let R1= 2 Ω, R2= 4 Ω, R3= 5 Ω
If the equivalent resistance is R, then 1/R = 1/R1 + 1/R2 + 1/R3 = 1/2 + 1/4 + 1/5 = 10+5+4/20 = 19/20
R = 20/19 = 1.05 Ω
- (b) The EMF of the battery = 20 V
Current through R1, I1 = V/R1 = 20/2 = 10 A
Current through R2, I2 = V/R2 = 20/4 = 5A
Current through R3, I3 = V/R3 = 20/5 = 4 A
Total current I = I1 + I2 + I3 = 10 + 5 + 4 = 19 A
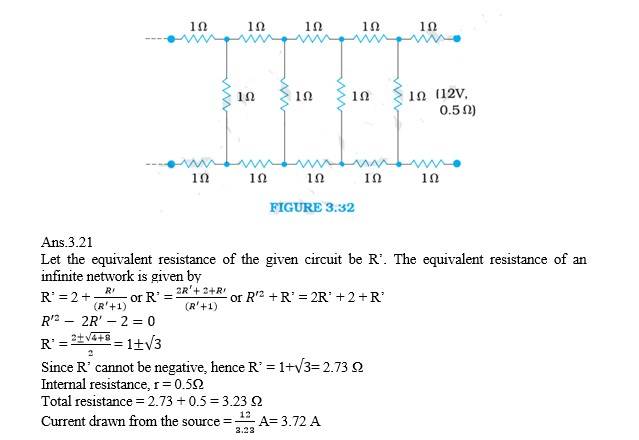
Q. Determine the current drawn from a 12V supply with internal resistance 0.5 Ω by the infinite network shown in Fig. 3.32. Each resistor has 1Ω resistance
News & Updates
Current Electricity Exam
Student Forum
Popular Courses After 12th
Exams: BHU UET | KUK Entrance Exam | JMI Entrance Exam
Bachelor of Design in Animation (BDes)
Exams: UCEED | NIFT Entrance Exam | NID Entrance Exam
BA LLB (Bachelor of Arts + Bachelor of Laws)
Exams: CLAT | AILET | LSAT India
Bachelor of Journalism & Mass Communication (BJMC)
Exams: LUACMAT | SRMHCAT | GD Goenka Test
