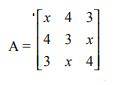Singular Matrix: Overview, Questions, Preparation

Matrix is an ordered array of numbers and elements that can be arranged in different manners. Each number or variable in the matrix is called elements. The size of a matrix is determined by the number of rows and columns in it. It is also known as the dimension of the matrix. The below-given figure is an example of the singular matrix.

Source: NCERT

Any matrix having a determinant as 0 is called a singular matrix. This type of matrix doesn't have any multiplicative inverse, i.e., they are non-invertible. There are broadly two types of matrix: a singular matrix and a non-singular matrix. As discussed earlier, the singular matrix has determinant 0, and the non-singular matrix has a determinant as a non-zero value.

Why do we use a singular matrix?

The matrix may seem a little weird mathematical concept, but that is what makes it different. It is one way to store numerical values uniquely and solve them for any given linear equations. They are essentially used to store information such as name, roll number, which can be retrieved easily when required.

What is the order of any matrix?

Finding the order of any given matrix is easy, as it involves counting the number of rows and columns. Then multiply the number of rows and columns with each other to define the order of the matrix.

Significance of singular matrix

Since the singular matrix has determinant 0, it acts as the intermediary between the positive and negative determinant matrices. They separate both entities.

When multiplied with a positive determinant matrix, the result leads to preserving the orientation of the matrix.

Vanishing probability is a thing that supports the singular matrix concept.

Matrix forms an integral part of the board syllabus. It is an essential topic for any entrance exams like JEE, NEET, etc. In class 12^th NCERT, you get familiar with the different matrix varieties and their properties. You also learn about the determinant and the multiplicative inverse concept of the given matrix.

1: For the singular matrix A, (A′) ^–1 = (A^–1)′. Is state true or false?

Solution: False we know that the singular matrix is non-invertible.

2: If A and B are two skew-symmetric matrices of the same order, AB is a symmetric matrix.

Solution: AB = BA

3: What is the determinant of any given singular matrix?

Solution: The determinant of any given singular matrix is always 0.

Q: How can we tell the difference between any singular matrix and non-singular matrix?

Q: What is the multiplicative inverse of a singular matrix?

Q: Suppose you are given a matrix of dimension 5 * 6. Then what is the order of the matrix?

Q: Is finding the multiplicative inverse of the given matrix easy?

Q: Which exams ask matrix questions?